NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
如果你的线性代数课和我的类似,你就会学到如何通过计算行列式来描述矩阵。然而,我发现大多数课程都没有完全定义矩阵行列式到底是什么。在这次讨论中,我希望深入探讨如何计算行列式,同时也描述你正在计算的内容。
1、定义
行列式是与方阵相关的标量值。让我们看看一般情况,看看我们如何计算行列式:

我们将此表达式称为拉普拉斯展开式(Laplace Expansion)。这里有很多东西需要解开,但一旦你掌握了符号表示,它就相当简单了。它基本上是说将矩阵 A 分成越来越小的子矩阵,直到你可以相对轻松地计算出行列式。我们还通过 A 的第 i 列和第 j 列为每个后续子矩阵添加一个“权重”。我们将在 3x3 的情况下研究这个概括。但首先让我们讨论最简单的计算 - 2x2 的情况:
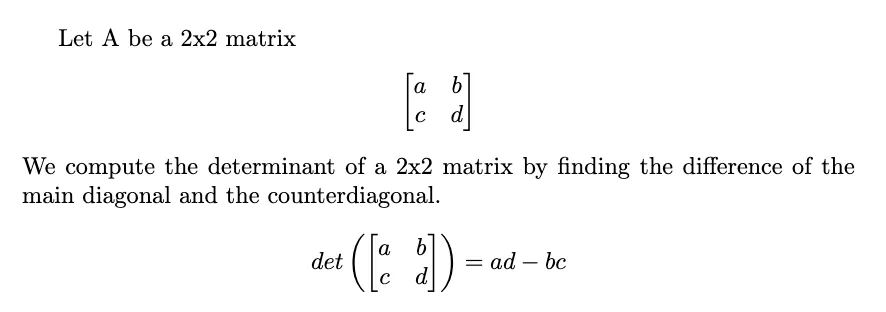
2x2 的情况只需找出主对角线和反对角线之间的差值。拉普拉斯展开式中的子矩阵可以简化为 2x2 的情况。但是,你也可以将子矩阵简化为 3x3 的情况:

请注意,3x3 的情况是拉普拉斯展开的直接应用。我们保持顶行固定(但可以是任何行或列),将其用作乘数,并将主矩阵简化为 2x2 子矩阵。由于我们可以轻松计算 2x2 子矩阵的行列式,因此计算变得更加简单。注意交替的正负号也很重要。这来自拉普拉斯展开中的 -1 项。我们在创建子矩阵时交替使用符号。
手动计算行列式很快就会变得不可行。想象一个 100x100 的矩阵。我们需要多次递归执行拉普拉斯展开,导致项激增。即使在较小的矩阵(例如 5x5 矩阵)中,它也很快变得平凡。但是,软件中的数值方法可以快速计算行列式,因此在大多数情况下不需要手动计算。
2、几何解释
行列式的代数解释非常适合为计算行列式提供基础。但是,它无法提供对行列式的直观理解。它使行列式看起来只是数字的乘积。
地理解释在解释行列式方面做得更好。让我们探讨 2x2 的情况:

上面是矩阵 A 的 2x2 描述。上面的平行四边形是通过认识到矩阵 A 形成两个线性映射而构建的:一个将标准基向量映射到 A 的行,另一个将标准基向量映射到 A 的列。换句话说,我们可以绘制图中所示的 A 的元素。
这使得行列式成为平行四边形的面积!那么,面积就代表了 A 变换其他面积的比例。现在我知道你在想什么了。
但行列式可以为负数。面积怎么会是负数呢?
好问题!这引出了我们的下一个讨论主题:方向。当我们将符号应用于面积时,我们就得到了一个有向面积。有向面积和面积之间的唯一区别就是符号:负向面积意味着第一和第二个向量的角度是顺时针方向而不是逆时针方向。但是,两者的面积大小是相同的。它们是具有大小和方向的类似向量。向量没有负大小;它只是具有与大小相关的方向。
好的,这描述了 2x2 的情况。那么 3x3 的情况呢?或者 NxN 的情况呢?答案是,它们是相同的概念!唯一改变的是形状。在 3x3 的情况下,它形成一个平行六面体,在 NxN 的情况下,它形成一个平行四面体。换句话说,3x3 的情况计算体积,4x4 的情况计算超体积,等等。在三维以上,它变得更加抽象,但基本原理保持不变:我们正在计算 A 变换其他物体的尺度。
3、行列式的属性
让我们回顾一下行列式的一些属性。其中许多属性可以通过上面的代数公式推导出来。我不会直接推导这些属性,但通过 2x2 的情况来验证这些属性中的每一个是一个很好的检查。
- 当两行交换时,行列式会改变符号。
- 如果两行相等,则行列式为零。
- 从一行中减去另一行的倍数会留下相同的行列式。
- 如果矩阵是奇异的,则行列式为零。
- AB 的行列式是 det(A) * det(B)
- A 的转置具有与 A 相同的行列式
4、行列式的应用
行列式有多种应用,但其中三种值得讨论。
- 奇异矩阵
确定矩阵是否非奇异(即可逆)的较简单方法之一是计算其行列式。奇异矩阵不可逆当且仅当行列式为零时。在线性代数中,知道矩阵是否可逆通常非常有益。
- 克莱默规则
有人可能会说,线性代数的主要目标是解方程:

克莱默规则(Cramer's Rule)是计算 x 的一种方法。我们将 x 的第 j 个分量定义为:

其中 B 与 A 相同,只是 a 中的第 j 个分量被向量 b 替换。虽然克莱姆法则是一种有趣的解决问题的方法,但从计算复杂性的角度来看,它效率极低。有更多更有效的算法可用于计算 x。
- 特征方程
线性代数中的特征方程是:

它用于确定矩阵 A 的特征值和特征向量。虽然特征值和特征向量有点超出了本文的讨论范围,但它们在线性代数之外的许多数学领域中都发挥着重要作用。关于行列式,请注意,我们直接计算上述表达式的行列式。我们还找到了特征值,使得表达式是一个奇异矩阵,这是它成为特征值的必要条件。
5、Python 中的行列式
如前所述,手动计算很繁琐,而且很容易出错,效率低下。Python 和 Matlab 等编程语言能够高效准确地计算行列式。让我们看一个例子:

我们可以使用拉普拉斯展开式将矩阵划分为 3x3 子矩阵,然后将其划分为 2x2 子矩阵,但请注意我们需要跟踪多少项。我们还需要确保每个项的符号与展开式保持一致。但是,如果你只需要找到行列式,还有一种更简单的方法:python!
import scipy.linalg as la
import numpy as np
A = np.array([[2,4,2,5], [1,5,2,6], [8,5,3,2], [0,1,3,6]])
det = la.det(A)
快速而简单。我们能够高效而准确地计算矩阵的行列式。4x4 矩阵相对较小,但你能想象如果我们有一个 10x10 矩阵会怎样吗?100x100 矩阵?1000x1000 矩阵?编程语言成为大多数应用程序的唯一选择。
6、结束语
行列式很难解释。学习如何计算矩阵并使用其属性来描述矩阵要容易得多。直观地了解你正在计算的内容要困难得多。希望这有助于让你获得这种直观的理解。
原文链接:Deep Dive into Matrix Determinants
BimAnt翻译整理,转载请标明出处