NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
FEA 是 Finite Elements Analysis(有限元分析)的首字母缩写。基于有限元方法(FEM),它是一种利用计算机预测不同类型物理系统(如固体变形、热传导和流体流动)的行为的技术。FEA软件,或FEM软件,是工程师和物理学家使用的非常流行的工具,因为它可以将物理定律应用到现实生活中的场景,并保持一定的精度、功能性和实用性。在这篇文章中,我们将介绍 FEA 初学者需要了解的内容。
1、FEA 是如何工作的?
FEA 是将有限元方法 (FEM) 应用于实际问题。有限元法是微分方程近似求解的过程,其目标是将微分方程转换为一组线性方程,然后由计算机以常规方式解决。

微分方程非常重要,在许多工程问题中都可能需要使用微分方程来表示物理定律。这些微分方程将物体内部变量的变化(如位移、温度或压力)与物体的几何形状、物理属性和外部影响关联起来。
如何将微分方程转换为一组线性方程的详细解释超出了本文的范围,但下面是此过程的一般概述:
- 恰当地定义物理问题,以微分方程的形式应用物理定律。
- 恰当地定义待分析对象的几何形状,其占用的空间称为"域",封闭表面称为"边界"。
- 恰当地定义作用于边界或域上的外部影响,例如力、压力、温度或热源。这些被称为"边界条件"。
- 恰当地定义对象的"初始条件"。这些是待分析问题初始时刻地内部变量的值的集合,例如初始速度、预应力或初始温度分布。
- 域被分割成小的基本形状,称为"元素"或"元"(Element)。元素集合被称为"网格"(Grid)。此外,邻居的元素的交点称为"节点"(Node)。元素的大小将决定近似解的精度,显然元素定义定义地越小越好。但是,元素数量越多,对内存和处理器时间等计算资源的需求也就越大。
- 方程和边界条件都被"映射"到节点中,从而得到有限 — 但往往是大量 — 的线性方程。
- 线性方程由计算机求解,并将每个节点和元素的结果变量写入文件。
- 生成的数据可用于进行数字分析、可视化和设计决策。

2、FEA 的应用案例
虽然有限元法与具体的物理问题类型没有关系,但其主要应用领域是固体结构分析。结构分析可能包括不同类型的载荷和场景,但它的主要目的是:预测指定的部件或结构是否能够安全地承受对其起作用的力量。
这是根据材料的抗性理论,通过从应力和应变的角度观察部件的状态来实现的。将任何方法(例如FEM)获得的最大值与允许的值进行比较,以查看这些值是否符合安全范围。这些允许的值范围大部分是由相关规范(如 ASCE、ASME、Eurocode等)指定的。
FEA 软件的一些典型使用案例包括:
- 钢筋混凝土结构,用于建筑物和其他民用应用、起重等。
- 工业设备,如压力容器、管道、锅炉、旋转设备等。
- 制造设备,如磨坊、模具、工具等。
- 汽车、飞机或其他运输结构,特别是虚拟碰撞测试。
3、压力和应变简介
在开始使用 FEA 进行结构评估之前,需要了解的两个非常重要的概念是应力和应变,因为它们都与固体的变形有关。在学习材料强度相关的知识时,通常会深入讨论这些主题,但在这里我们将仅作简短的介绍。
当固体受到外部力量(如压力、接触或重力)的作用时,固体会经历一些变形。这种变形的形状和大小取决于许多因素,如外力的方向和大小、固体的几何形状和构成材料的刚性。
最简单的例子是弹簧的变形:当弹簧悬挂在垂直位置时,它处于具有一定特征长度的平衡状态。如果重量附加到底端,弹簧将延伸,直到达到另一个平衡点,这一次更长的长度。

如果改变底端重量的大小,我们会注意到,弹簧的拉长与重量成正比,这也称为胡克定律,恒定的比例被称为弹簧的"刚性"。
4、什么是应力?
当固体外部受力时,由材料内部形成的力对抗了外力,导致平衡状态。这些内力被称为材料的"应力",是分子水平上凝聚力的结果。外力的活动越高,材料所形成的压力就越大。失败理论基于应力的极限,即当压力水平超过给定阈值时,将导致元素的失败。
5、什么是应变?
在试图用材料应力来书写胡克定律时,人们注意到元素的拉长并不是一个一致的衡量标准。如果测试标本的几何形状(例如,单轴测试)被更改,则刚度常数不会一般化为给定材料。注意到的是,应考虑一种特殊的变形措施。这被称为材料"应变",并有几个不同的定义,如"工程应力"或"真正的压力"。这些定义允许使用称为杨氏模量的材料刚性测量来说明材料应力和应变之间的关系。

同样重要的是要注意,即使压力和变形是FEA的主要目标计算,它们也不是唯一可以用它做出的重要预测。对于可以通过 FEA 获得的特定结构系统的其他非常有用的信息包括:
- 自然振动频率和模式
- 强制振动(谐波)响应
- 薄结构的弯曲限制和模式
- 断裂传播模式与疲劳寿命
6、使用 FEA 的关键行业
- 汽车
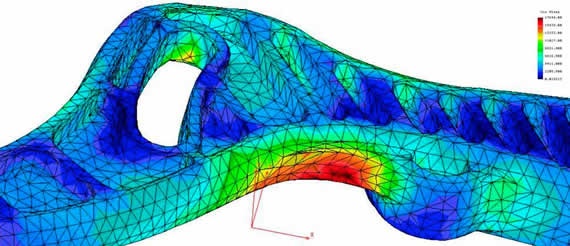
在汽车行业, FEA 软件模拟旨在评估设计部件(如底盘、锚、悬架、车身等)的结构安全性。其中一个最有趣的应用是虚拟碰撞测试,改测试是通过动态模拟,以预测对碰撞冲击的变形和能量吸收。这里是汽车悬架的变形和压力:

- 工业设备
在工业设备设计和工程方面,有限元分析软件被广泛应用。例如,在加工业中,压力和热负荷用于预测管道、压力容器、储罐和类似设备的压力水平。FEA在该行业的另一个可能用途是仿真锻造工艺,以测量锻造部件的应力等级。
- 土木工程和结构设计
在土木工程和结构设计方面,FEA 软件释放了快速准确分析的威力,可以自动应用程序化负载组合并检查合规性。典型的分析场景包括静态加载、等效静态加载、地震场景中的动态性能、自然振动模式和频率计算。下面是一个对钢结构进行结构分析的项目示例:

7、为什么 FEA 很重要?
FEA 是用于几乎所有工程领域进行详细地应力分析和变形预测的事实技术。随着设计师和工程师能够使用更多的分析工具,FEA也将有更大的空间来扩大其影响力。正如我们已经看到的,FEA非常通用并且强大,这使它成为任何产品设计组合中必备的工具。
原文链接:FEA For Beginners
BimAnt翻译整理,转载请标明出处