NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
过去 50 年来,3D 渲染技术取得了重大进步,并且越来越多地出现在我们的日常生活中:当今的路径追踪算法在电影中随处可见,而大多数视频游戏都使用光栅化程序来处理图形。
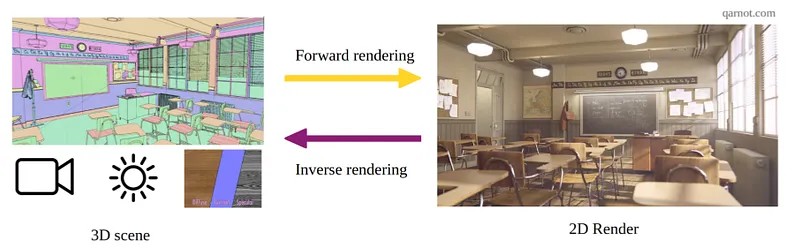
虽然这些技术越来越接近真实感,但另一个问题出现了:如果我们不是从 3D 场景到 2D 图像(渲染),而是从 2D 图像到 3D 场景,会怎样? 正如你可能想象的那样,从 2D 信息重建 3D 场景相当复杂,但在过去几年中已经取得了许多进展。 这个研究领域称为逆向图形学(inverse graphics)。
本文介绍的可微渲染(DR:Differentiable Rendering)方法属于用于解决逆向图形问题的方法。
1、什么是可微渲染?
3D 渲染可以定义为一种将 3D 场景作为输入并输出 2D 图像的函数。 可微渲染的目标是提供可微渲染函数,也就是说计算该函数对于不同场景参数的导数。
你可能想知道为什么我们需要可微的渲染函数:许多优化技术都使用导数。 例如,梯度下降算法使用导数来调整参数,并且通过使用梯度反向传播技术调整权重来训练神经网络。
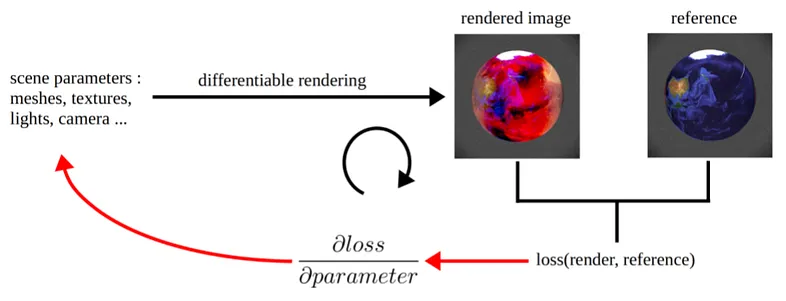
一旦渲染器可微分,它就可以集成到优化或神经网络管道中。 然后,这些管道可用于解决逆向图形问题,例如从 2D 图像进行 3D 重建或光传输优化任务。
许多前向渲染算法(相对于逆向渲染算法)在设计时并未考虑到微分,遮挡等现象会引入许多不连续性,并且在光栅化算法中几乎每个步骤都是不可微分的。 虽然颜色或光泽度等参数的导数可能很容易获得,但顶点位置或物体方向等几何参数的微分通常需要改变图像的计算方式。 设计强大且高效的可微渲染方法是计算机图形学研究的一个活跃领域。
在过去的 10 年里,研究人员发布了使用光栅化或光线追踪的可微渲染器以及许多实验性应用程序。
2、可微渲染应用于路径追踪
路径追踪(Path Tracing)是 CGI 行业广泛使用的一种渲染技术,它使用光线追踪来渲染图像。 Arnold、Redshift 或 Blender Cycles 等知名渲染器都在使用此算法。 路径追踪是一种生成逼真图像的出色技术:模拟空间中的光传输使我们能够考虑全局照明或反射等效果。
我们的目标是了解路径跟踪的工作原理以及如何构建可微的路径跟踪器。
3、路径追踪如何工作?
路径追踪是光线追踪的一种变体:通过来自相机的光线来模拟光在空间中的传播。 路径追踪技术背后的想法是 James Kaijya 在他 1986 年的论文the rendering equation中提出的。 渲染方程可以写成:
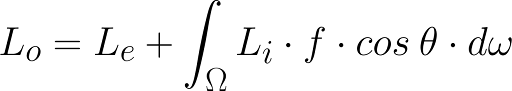
其中:
- Lo :某一点的光强度(辐射率)
- Le :此时发出的辐射亮度
- Li : 到此点的入射光亮度
- f :双向反射分布函数 (BRDF),用于量化光的反射方式
- theta :传入方向 (?) 与表面法线之间的角度
使用的相机模型是针孔相机模型。 相机由其原点和图像平面定义。 图像平面被细分为与渲染分辨率相对应的像素网格,并且光线从相机的原点通过图像平面的像素发射。 图 1 说明了相机的工作原理。
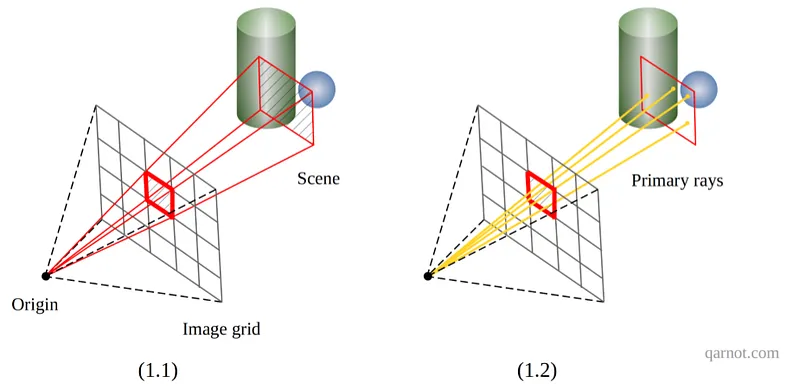
既然图像平面已经转化为像素网格,那么每个像素的颜色是如何收集的呢? 通过场景传播像素的边界会突出显示包含多个对象的场景的大区域,所有这些对象都会影响像素的最终颜色。 要计算该颜色,必须考虑通过像素的所有光线。
从数学上讲,这对应于对像素区域上的光强度(辐射率)进行积分。 由于定义场景的函数非常复杂,因此该积分计算起来非常复杂且昂贵。 蒙特卡洛估计器将用于计算该积分的值:N 条光线将随机穿过像素发射到场景中并评估它们的光强度。 该操作如图1.2所示。图像网格中位置(i,j)处的像素辐射亮度值可写为:
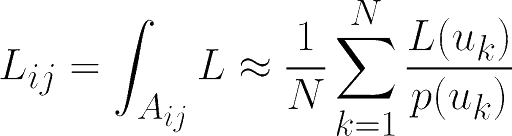
其中:
- p :用于用射线对像素空间进行采样的概率分布函数
- uk :随机射线。
从相机进入场景的光线称为主光线(primary rays)。 一旦这些光线与场景几何体相交,它们就会在空间中传播。 在每个交叉点,通过求解渲染方程来估计交叉点处的光强度。
一条光线(单个样本)从该交点发射到场景中。 虽然每个像素发射一条光线不会给出精确的结果,但每个像素发射多条光线将给出入射光的良好近似值。
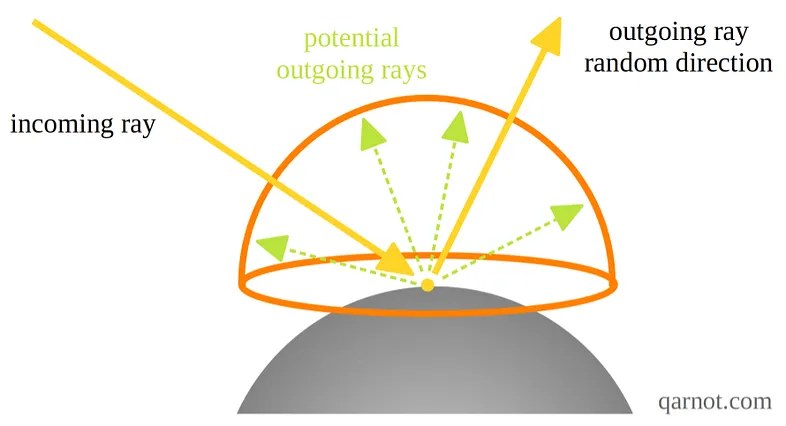
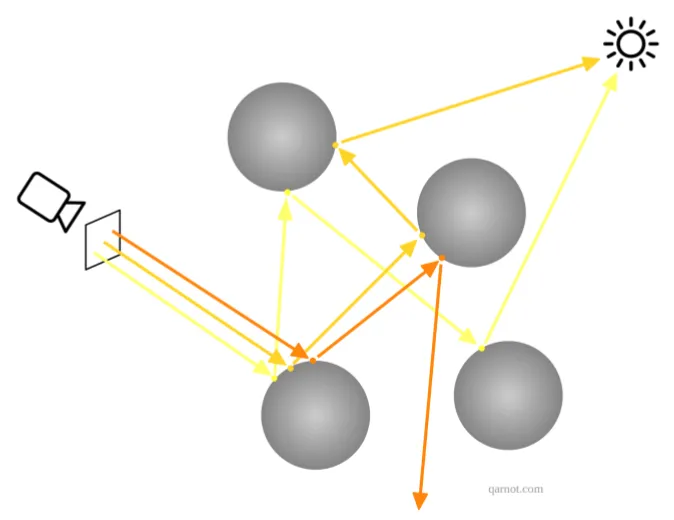
均匀采样(Uniform Sampling)可用于选取光线,但生产路径追踪器使用基于对象材料特性的重要性采样(Importance Sampling)方法,以大幅减少图像中的噪声并提高收敛性。 光线不断反弹,直到遇到光源或达到光线深度限制(最大反弹次数)。 图 3 说明了此过程。
4、路径追踪与微分
现在我们知道了如何通过路径追踪来渲染图像,让我们来解决渲染函数的微分问题。
总结前面的部分,路径追踪的渲染函数由使用蒙特卡罗方法估计的嵌套积分组成。 当我们根据场景参数对这个函数进行微分时,我们遇到的主要障碍将来自于这些积分的微分。
首先,我们不要忘记何时以及如何对积分进行微分。 为了区分函数 f 在域 D 上关于其参数 p 之一的积分,函数 f 必须满足以下要求:
- f 必须关于 p 连续
- df/dp 必须相对于 D 上的 p 连续。
该条件也可以表示为 f 属于 C1(D) 类。 准确地说,我们在研究中要处理的函数是分段连续的,为了使前面的性质有效,函数必须满足其每个子域的连续性条件,并且这些子域的边界不得依赖于参数 p。
让我们区分一个像素的渲染函数 f 相对于场景参数 p(p 可以是对象的颜色、位置等)。对像素点的光强值求导的第一步是对像素点积分进行微分:
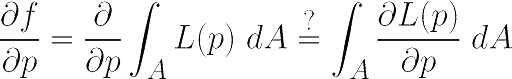
为了能够继续该步骤并用具有微分被积函数的积分替换微分积分,入射光函数 L 及其导数 dL/dp 必须在积分域 A(像素区域)上连续 参数p,即L属于C1(A)。 这一点是可微路径追踪器的关键。
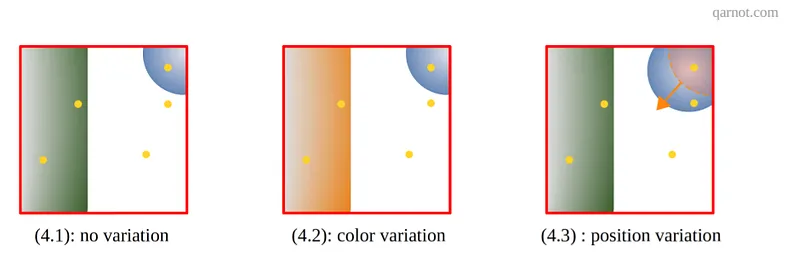
让我们回顾一下某些类型的场景参数和入射光函数 L 的连续性。为了解释这些积分微分所产生的问题,我们将借鉴 Loubet 等人的解释。我们必须回到 “像素视图”区域用于说明各类参数对积分的影响。 颜色参数(以及扩展纹理)的变化不会影响“像素视图”区域中的不连续性,因此可以对被积函数进行微分。 然而,当物体或灯光位置等几何参数发生变化时,“像素视图”区域中不连续的位置也会发生变化。 这些参数不满足连续性条件。 图 4 说明了这一点:(4.2) 表示颜色参数,(4.3) 表示几何参数。
如果满足这个条件(连续性),微分就非常简单:可以使用蒙特卡罗方法以类似于前向路径追踪的方式估计 dL/dp 的积分。 可以写成如下:
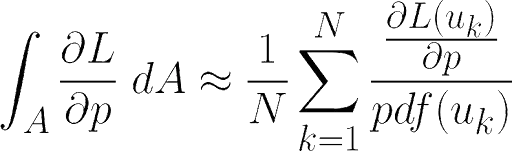
其中:
- pdf :用于用射线对像素空间进行采样的概率分布函数
- uk :随机样本。
但是,如果不满足这些连续性条件,则无法轻松计算导数。 这个主题(关于几何参数微分光积分)是一个活跃的研究主题,不同的研究人员提出了各种方法来解决这个问题,其中两种方法将在下面的段落中介绍。
Loubet 等人提出了第一个根据几何参数区分入射光的解决方案。 在他们的论文Reparameterizing discontinuous integrands for differentiable rendering中,通过光积分变量的变化来处理几何不连续性的问题。 一旦从积分中消除了不连续性,就可以使用蒙特卡罗方法进行估计。 该方法已集成到 Mitsuba 2 渲染器中,并且将是我们稍后在示例中使用的方法。
第二种解决方案,由 Li 等人提出。 在他们的Differentiable Monte Carlo Ray Tracing through Edge Sampling论文中,使用雷诺传递定理将积分的导数转换为连续积分和边界积分。 在计算导数时需要边界积分来考虑几何不连续性。 如果满足连续性条件,则可以使用所用的相同技术来估计这两个积分中的第一个。 通过对场景对象的轮廓边缘进行采样来评估边界积分。
5、结束语
在本文中,我们研究了路径跟踪渲染算法并解释了如何构建可微的路径跟踪器。
可微的路径追踪器将允许将先进的光传输模拟集成到优化管道和神经网络中。 Mitsuba 2 可微路径追踪器在 Qarnot 上的实现和两个实验将在即将发布的第二篇文章中介绍!
原文链接:An overview of Differentiable Rendering
BimAnt翻译整理,转载请标明出处