NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
法线(Normal)在着色(Shading)中起着核心作用。在本文中我们将介绍法线的基本概念,了解面法线和顶点法线的不同作用,并学习基于面法线和顶点法线的不同着色技术。
每个人都知道,如果我们将物体指向光源,物体就会变得更亮。物体表面的方向在它反射的光量(因此它看起来像多亮)中起着重要的作用。此方向可由物体表面任意一点P的法线N(Normal)表示:
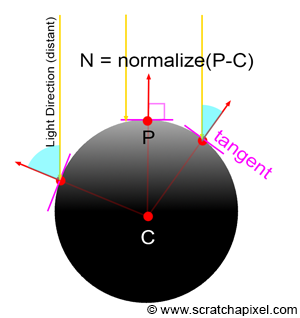
请注意上图 中,当光线方向和法线方向之间的角度增加时,球体的亮度是如何降低的。我们将在稍后解释这一现象的原因。现在只需要记住:
- 我们所说的法线(我们用大写字母表示)N是垂直于点P处表面切线的向量。换句话说,要计算P点的法线,我们需要在P点画出切线,然后找到垂直于切线的适量。
- 物体表面一个点的亮度取决于该点处的表面法线与光线方向的关系。另一种说法是,物体表面任何给定点的亮度取决于此处法线与光线方向之间的角度。
现在的问题是,我们如何计算这个法线?此问题解决方案的复杂性因几何类型而异。球体的法线通常很容易找到。如果我们知道球体表面点的位置和球体中心的位置,则此处的法线可以通过如下简单代码得到:
Vec3f N = P - sphereCenter; 如果对象是Mesh网格,则每个三角形定义了一个面,垂直于这个面的向量就是三角面上的任何一个点的法线。与三角面垂直的矢量很容易通过三角面的两边叉积得到。请记住,v1 * v2 = -v2 * v1。因此,边的选择将影响法线方向。如果你按逆时针顺序声明三角形顶点,则可以使用以下代码:
Vec3f N = (v1-v0).crossProduct(v2-v0); 如果三角形位于 xz 平面中,则法线应为 (0,1,0),而不是(0,-1,0):
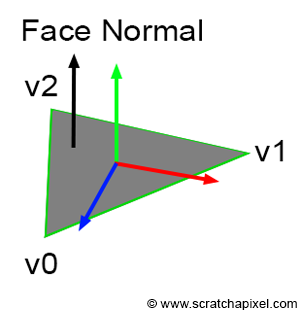
a上面给出的计算法线的方法就得到 面法线,因为在整个平面上法线都是相同的,无论你选择哪一点。三角网格的法线也可以在三角形的顶点上定义,在这种情况下,我们称之为 顶点法线 。顶点法线用于一种被称为平滑着色(Smooth Shading)的技术,我们将在后面部分介绍。现在,让我们聚焦于面法线。
在程序中如何以及何时计算表面需要着色的点的法线并不重要。重要的是,当你即将对点进行着色时,手头有这些信息。在本节的几个程序中,我们进行了一些基本的着色,我们在每一个几何类中都实现了一个特别的方法 getSurfaceProperties() 来计算交叉点的法线和其他变量(如纹理坐标),我们将在此课程的稍后部分讨论这些变量。以下是球体和三角网格的 getSurfaceProperties() 的实现代码:
class Sphere : public Object
{
...
public:
...
void getSurfaceProperties(
const Vec3f &hitPoint,
const Vec3f &viewDirection,
const uint32_t &triIndex,
const Vec2f &uv,
Vec3f &hitNormal,
Vec2f &hitTextureCoordinates) const
{
hitNormal= Phit - center;
hitNormal.normalize();
...
}
...
};
class TriangleMesh : public Object
{
...
public:
void getSurfaceProperties(
const Vec3f &hitPoint,
const Vec3f &viewDirection,
const uint32_t &triIndex,
const Vec2f &uv,
Vec3f &hitNormal,
Vec2f &hitTextureCoordinates) const
{
// face normal
const Vec3f &v0 = P[trisIndex[triIndex * 3]];
const Vec3f &v1 = P[trisIndex[triIndex * 3 + 1]];
const Vec3f &v2 = P[trisIndex[triIndex * 3 + 2]];
hitNormal = (v1 - v0).crossProduct(v2 - v0);
hitNormal.normalize();
...
}
...
}; 简单着色效果:面比率/Facing Ratio
现在,我们知道如何计算物体表面一个点的法线,已经有足够的信息来创建一个简单的着色效果,面比率 ,即 Facing Ratio。此技术计算待着色点的法线和查看方向的点积。计算查看方向也非常简单。当使用射线跟踪(Ray Tracing)方法时,查看方向就是与表面P点相交的光线的相反方向,在不使用射线跟踪时,还可以通过从表面上的点P跟踪到眼睛E的线来找到查看方向:
Vec3f V = (E - P).normalize(); // or -ray.dir if you use ray-tracing 请记住,如果两个向量平行并指向同一方向,则其点积返回 1,当两个向量相互垂直时则点积返回 0。如果向量指向相反的方向,则点积为负值,但如果我们使用此时的点积结果,颜色值就是负的,这时我们需要将结果压缩为 0:
float facingRatio = std::max(0, N.dotProduct(V));
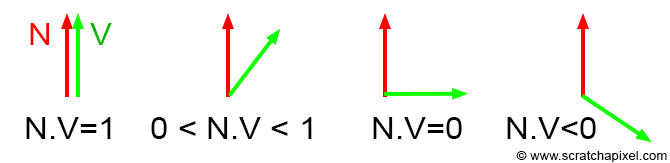
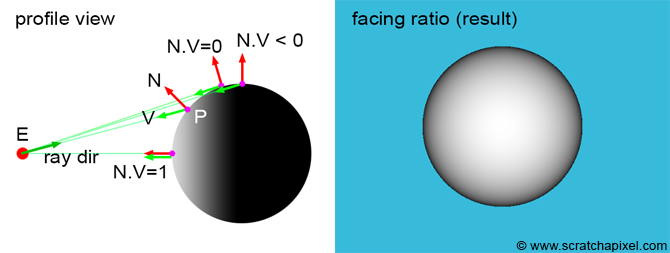
当法线和矢量V指向同一方向时,点积返回1。如果两个矢量垂直,则结果为 0。如果我们使用这种简单的技术来着色框架中心的球体,那么球体的中心将是白色的,当远离中心时,球体会变暗,如下图所示:
Vec3f castRay(
const Vec3f &orig, const Vec3f &dir,
const std::vector<std::unique_ptr<Object>> &objects,
const Options &options)
{
Vec3f hitColor = options.backgroundColor;
float tnear = kInfinity;
Vec2f uv;
uint32_t index = 0;
Object *hitObject = nullptr;
if (trace(orig, dir, objects, tnear, index, uv, &hitObject)) {
Vec3f hitPoint = orig + dir * tnear; // shaded point
Vec3f hitNormal;
Vec2f hitTexCoordinates;
// compute the normal of the point of we want to shade
hitObject->getSurfaceProperties(hitPoint, dir, index, uv, hitNormal, ...);
hitColor = std::max(0.f, hitNormal.dotProduct(-dir)); // facing ratio
}
return hitColor;
} 恭喜!你刚刚了解了第一种着色技术。现在让我们来了解一个更逼真的着色方法,它将模拟光对漫射物体的影响。但在了解这种方法之前,我们首先需要介绍和学习光的概念。
平面着色 vs. 平滑着色
三角面网格的问题在于它们不能表示完全光滑的表面(除非三角面非常小)。如果我们想要将刚才描述的Facing Ratio技术应用于多边形网格,我们需要计算射线相交的三角形的法线,并计算面法线和查看方向的点积。此方法的问题在于,它使对象具有以下图像中所示的面片化外观,这就是该方法被称为 平面着色(Flat Shading)的原因。
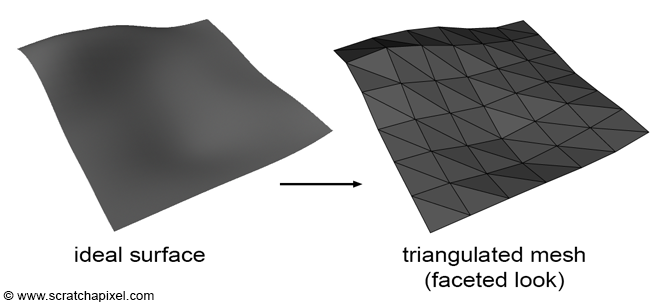
如前几次所述,只需计算矢量 v0v1 和矢量 v0v2 的叉积,即可找到三角面的法线,其中 v0、v1 和 v2 表示三角形的顶点。为了解决这个问题,Henri Gouraud在1971年引进了被称为 平滑着色 (Smooth Shading)的方法。此技术背后的理念是在多边形网格的表面产生连续阴影,尽管网格所代表的对象并不是连续的,因为它是从平面(多边形或三角形)集合中构建的。为此,Gouraud引入了顶点法线的概念。思路很简单,我们不计算或存储三角面的法线,而是为网格的每个顶点存储一个法线,法线的方向由三角网格的基础平滑表面决定。当我们想要计算三角面上一个点的颜色时不使用面法线,而是通过线性插值三角形的顶点法线性地插值,使用点的重心坐标来计算"伪平滑"法线值。该技术如下图所示:
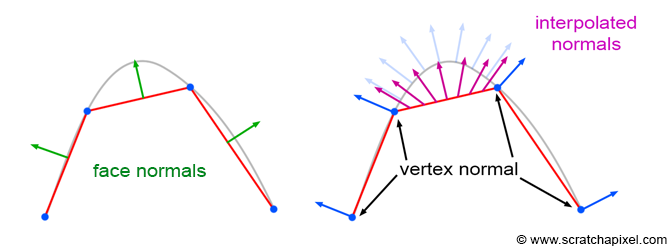
顶点法线在三角形顶点上定义。你可以看到,它们是垂直于三角面网格对应的原始光滑底层表面。有时三角形网格不是从光滑的表面直接转换来的,那么顶点法线必须实时计算。当没有平滑的表面时,存在多种计算顶点法线的技术,但我们不会在本文中研究这一点。现在你可以使用Maya或Blender等软件为你完成此工作(在Maya中,你可以选择多边形网格,并在"Normals"菜单中选择"Soften Edges"选项)。
事实上,从实用和技术的角度来看,每个三角形都有3个顶点法线。这意味着三角网的顶点法线总数实际上等于三角形的数量乘以 3。在某些情况下,2个或更多三角形共享的顶点上定义的顶点法线相同(指向同一方向),但可以通过设置其指向不同的方向来实现不同的效果(例如,你可以构造表面的伪硬边)。
只要我们知道三角形的顶点法线,三角形上的某个点的重心坐标以及三角形索引,那么插值计算三角形表面任何点的法线就很简单。无论是栅格化还是射线追踪都可以提供这些信息。顶点法线由 3D建模 程序生成,然后,它们被导出到几何文件中,其中包含了三角形连接信息、顶点位置和三角形纹理坐标。我们需要做的就是结合点的重心坐标和三角形顶点法线计算这个点的法线(下面的17-20行):
void getSurfaceProperties(
const Vec3f &hitPoint,
const Vec3f &viewDirection,
const uint32_t &triIndex,
const Vec2f &uv,
Vec3f &hitNormal,
Vec2f &hitTextureCoordinates) const
{
// face normal
const Vec3f &v0 = P[trisIndex[triIndex * 3]];
const Vec3f &v1 = P[trisIndex[triIndex * 3 + 1]];
const Vec3f &v2 = P[trisIndex[triIndex * 3 + 2]];
hitNormal = (v1 - v0).crossProduct(v2 - v0);
#if 1
// compute "smooth" normal using Gouraud's technique (interpolate vertex normals)
const Vec3f &n0 = N[trisIndex[triIndex * 3]];
const Vec3f &n1 = N[trisIndex[triIndex * 3 + 1]];
const Vec3f &n2 = N[trisIndex[triIndex * 3 + 2]];
hitNormal = (1 - uv.x - uv.y) * n0 + uv.x * n1 + uv.y * n2;
#endif
// doesn't need to be normalized as the N's are normalized but just for safety
hitNormal.normalize();
// texture coordinates
const Vec2f &st0 = texCoordinates[trisIndex[triIndex * 3]];
const Vec2f &st1 = texCoordinates[trisIndex[triIndex * 3 + 1]];
const Vec2f &st2 = texCoordinates[trisIndex[triIndex * 3 + 2]];
hitTextureCoordinates = (1 - uv.x - uv.y) * st0 + uv.x * st1 + uv.y * st2;
} 请注意,这只是看起来表面光滑。如果你看看下面图像中的多边形球体,仍然可以看到面片的轮廓,即使表面看起来光滑。该技术的确改善了三角网状的外观,但不能完全解决面片化问题。解决这个问题的唯一办法是使用 细分表面(subdivision surface),我们将在另一篇文章中讨论这一技术。此外,将光滑表面转换为三角网状时增加使用的三角形数量当然也可以使这一问题得到改善。

原文链接:Normals, Vertex Normals and Facing Ratio
BimAnt翻译整理,转载请标明出处





