NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
采购管理是一种战略方法,可在确定的预算范围内,在特定截止日期或之前从首选供应商处采购商品或服务。
我们的目标是以某种方式平衡供需,以确保最低水平的库存来满足商店需求。
在本文中,我们将介绍一种使用非线性规划的简单方法,为中型零售店设计最佳库存补货策略,考虑:
- 从供应商仓库到商店储备 的运输成本(美元/纸箱)
- 为你的库存提供资金的成本(以美元计的库存价值的百分比)
- 储备(商店的仓库)存储租金成本(美元/纸箱)
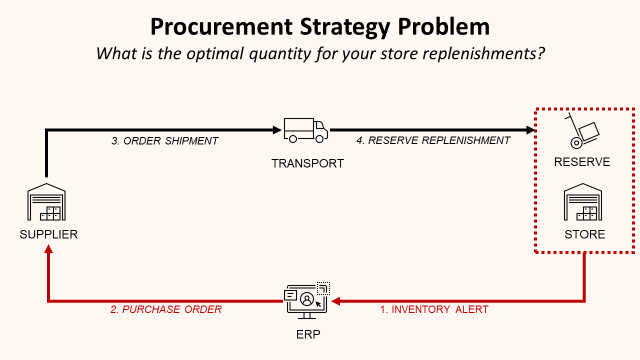
1、场景介绍
作为中型零售店的店长,您负责在 ERP 中设置补货数量。
对于每个 SKU,当库存水平低于某个阈值时,你的 ERP 将自动向您的供应商发送采购订单 (PO)。
你需要平衡库存能力、运输成本和库存成本的限制,为你的采购订单确定正确的数量。
- 1 个供应商通过 EDI 连接(使用你的 ERP)接收你的订单并使用第三方运输公司发货,费用由你承担
注意:我们不会在本文中考虑任何交货时间 - 60 个有效库存单位 (SKU),采购价格 ($/carton)和年销售量 (Cartons/year)
- 使用第 3 方公司进行运输,该公司运营按纸箱开具发票的包裹递送($/Carton)
- 存储位置(Store's Reserve),货架上存储容量为480 箱

为了简化理解,我们引入一些符号:
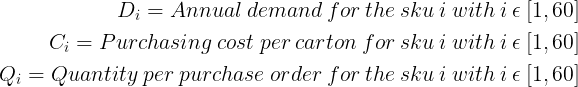
每个 SKU 的年需求量
运输:

b = 42.250 $
A = -0.3975 $/纸箱
资本成本

作为一家中型企业,我们假设你的资金成本相当高:12.5%。
存储成本

在这个模型中,我们假设我们拥有世界上最好的房东。她按每年的平均价值按纸箱向我们开具发票。我们不会为空置地点付费。
Imax= 480
Rmonth= 2,000 $/月
问题
你应该在 ERP 中设置多少每次补货 Qi以最小化总成本?
2、建立模型
与本系列的上一篇文章不同,我们不会使用 PuLP,因为我们不是线性规划问题。我们将使用 SciPy 优化函数来解决这个非线性最小化问题。
2.1 声明决策变量
你想决定什么?
我们想设置我们的 ERP 发送给供应商的每个补货订单的数量。
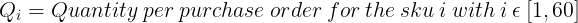
然而,为了简化我们的计算,我们将使用每年的补充数量Ri作为决策变量。

补货数量将使用以下公式计算。
注意:我们接受不是整数的补货箱数量。
2.2 声明目标函数
你想最小化什么?
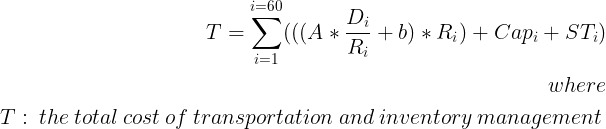
采购成本本身不包含在目标函数中,因为它超出了我们的优化目标范围。
代码
# Initialize constraints list
cons = []
# Maximum Inventory
def constraint1(R):
loop = 0
for i in range(60):
loop += R[i]
result = 480 - loop
return result
cons.append({'type':'ineq','fun':constraint1})
# Add Order Size Constraints
for i in range(60):
# Minimum Order Quantity
c2 = lambda R : (df_demand.loc[i,'DEMAND']/R[i]) - 1
cons.append({'type':'ineq','fun':c2})
# Maximum Order Quantity
c3 = lambda R : 400 - (df_demand.loc[i,'DEMAND']/R[i])
cons.append({'type':'ineq','fun':c3})2.3 定义约束
确定可行区域的资源限制是什么?
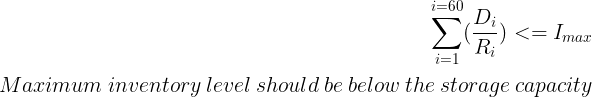
这是问题开始的地方,因为我们有一个非线性约束(1/Ri)。

2.4 求解模型并准备结果
你的模拟结果是什么?
初步猜测
与线性规划不同,我们需要为算法的第一次迭代提供潜在解决方案的初始向量来启动它。
在这里,我们假设所有 SKU 每年 2 次补货可能是一个不错的选择。
# All SKU replenished 1 time
R0 = [2 for i in range(60)]
print("${:,} total cost for initial guessing".format(objective(R0).round(1)))初始猜测的总成本为63,206.7 美元
希望最优解将是一个较低的结果。
求解:
# Initiate timer to measure procesing time
start = time.time()
# Create the solver using Sequential Least Squares Programming (SLSQP) method
sol = minimize(objective, R0, method = 'SLSQP', bounds=bnds, constraints = cons, options={'maxiter': 100})
exec_time = (time.time()-start)
print("Execution time is {}s for 100 iterations".format(exec_time))
# Solution: Inital Decision Variables
sol_init = sol.x
# Take the floor of the solution to have an integer as number of replenishment and never exceed stock limit
sol_final = [math.floor(i) for i in sol_init]
# Print total costs
print(('''For {} Iterations
-> Initial Solution: ${:,}
-> Integer Solution: ${:,}
''').format(100, sol.fun.round(1), objective(sol_final).round(1)))100 次迭代
初始解决方案:28,991.9 美元
整数解决方案:29,221.3 美元,最大库存为 356 个纸箱
3、结论和后续步骤
- 结论:对于所有参考,这种优化的解决方案比最初猜测的每年 2 次补货要好 56% 。
- 需求分布:如果我们对您的需求进行随机分布并且我们想避免缺货怎么办?在下面的文章中,您可以找到一种简单的方法来构建补货规则,假设您的需求是随机分布的。
- 下一步:我们可以在这里看到,我们的解决方案主要由运输成本驱动,因为我们最多有356 箱库存。
在下一篇文章中,我们将执行探索性数据分析,以了解我们的决策变量的分布,并了解是什么推动了每个参考的结果。
我们还将尝试了解从连续决策变量转换为整数决策变量的影响。
最后,我们将尝试几个场景来看看模型是如何反应的:
- 高租金和低运输成本
- 非线性采购成本
- 更高的最小订购量
原文链接:Procurement Process Optimization with Python
BimAnt翻译整理,转载请标明出处