NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
蒙特卡洛仿真(或概率仿真)是一种用于了解金融部门风险和不确定性、项目管理、成本和其他预测机器学习模型的影响的技术。
风险分析是我们做出的几乎每一个决定的一部分,因为我们经常面临生活中的不确定性、模糊性和多变性。此外,即使我们获得了前所未有的信息,我们也不能准确预测未来。
蒙特卡洛仿真使我们能够看到所有可能的结果,并评估风险影响,从而允许在不确定性下更好的决策。
在本文中,我们将通过五个不同的示例来理解蒙特卡洛仿真方法。本教程的代码可在Github及Google Colab 找到。
1、 掷硬币翻转示例
掷一个无偏硬币的正面向上的概率为 1/2。然而,我们有什么办法可以实验证明吗?在此示例中,我们将使用蒙特卡洛方法模拟掷硬币 5000 次,以找出为什么正面向上的概率始终为 1/2。如果我们重复掷这个硬币很多很多次,那么可以达到更高的准确性。
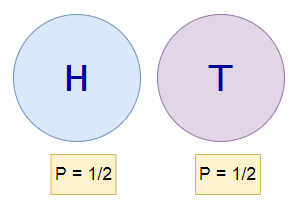
掷硬币时:
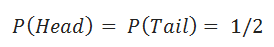
接下来,我们将用蒙特卡洛方法实验性地证明这个公式。
1、导入所需的库:
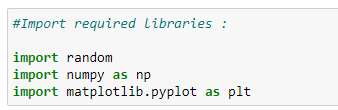
2. 掷硬币函数:

3.检查函数输出
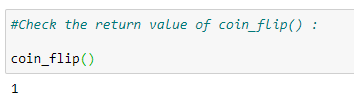
4、主函数:

5、调用主函数:
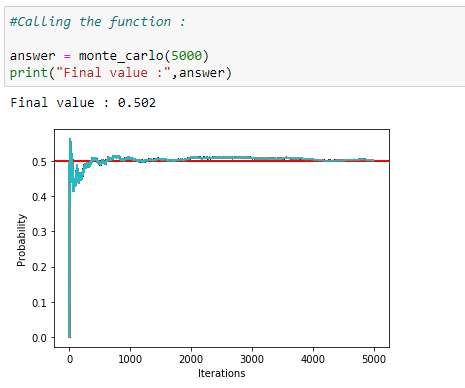
如上图所示,我们在 5000 次迭代后,获得正面向上的概率为 0.502。因此,这就是我们如何使用蒙特卡洛仿真来找到概率值的实验。
2、使用圆和正方形估计 PI
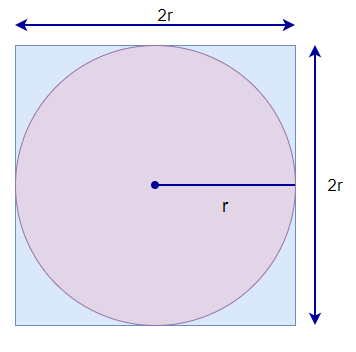
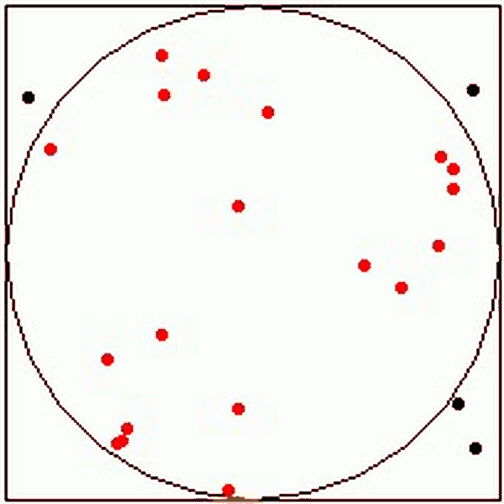
要估计 PI 的价值,我们需要正方型和圆的面积。为了找到这些区域,我们将随机将点放在表面上,并计算落在圆圈内的点和落在正方形内的点。这将给我们估计他们的面积。因此,我们将使用点计数作为区域,而不是使用实际区域的大小。
在以下代码中,我们使用 Python 的turfle模块来查看点的随机位置。
1、导入需要的库
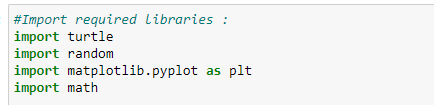
2、绘制点:
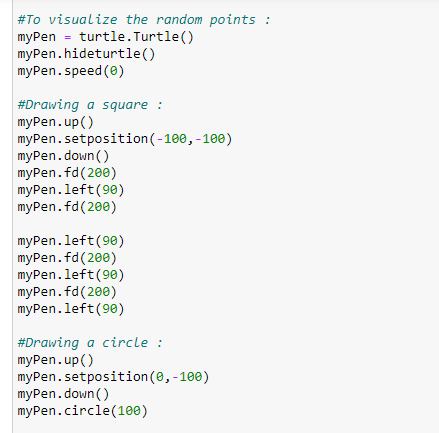
3、初始化必要的数据

4、主函数:

5、绘制数据图:

6、输出:
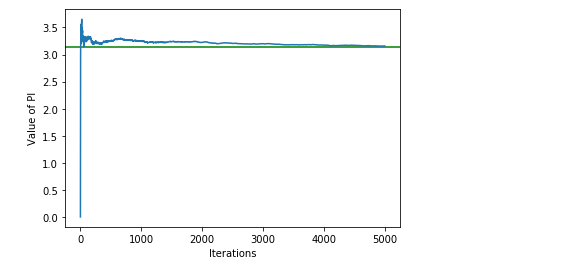
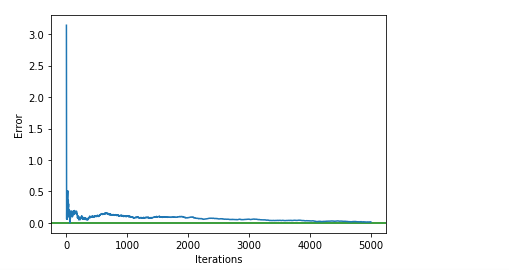
如上图 所示,经过 5000 次迭代后,我们可以获得 PI 的近似值。此外,请注意,随着迭代数的增加,估计误差也呈指数级下降。
3、Monty Hall问题
假设在一个游戏节目中, 你可以选择三扇门之一: 一扇门后面是一辆车; 其他门后面都是山羊。你挑一扇门,比方说门1,主持人,他知道门后面是什么,打开另一扇门,比如说门3,有一只山羊。主持人然后问你:你是要坚持你的选择还是选择另一扇门?
换门对你有利吗?
根据概率,换门对我们是有利的。让我们了解一下:
最初,对于所有三个门,获得汽车的概率(P)是相同的(P = 1/3)。
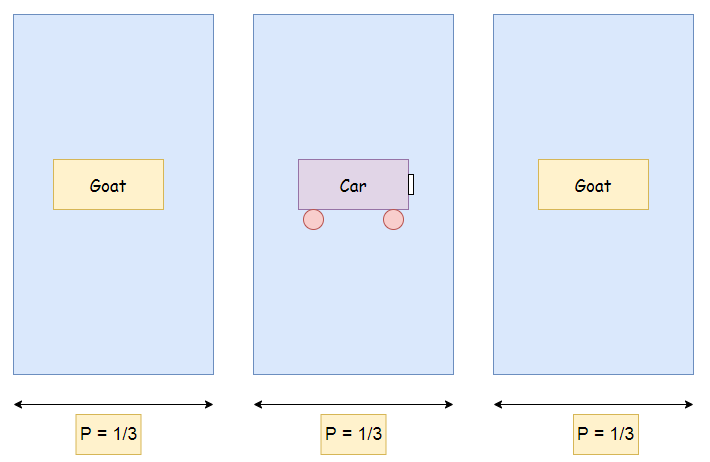
现在假设参赛者选择门 1。然后主持人打开第三扇门,门后面有一只山羊。接下来,主持人问参赛者是否想换门?
我们将看到为什么换门更有利:
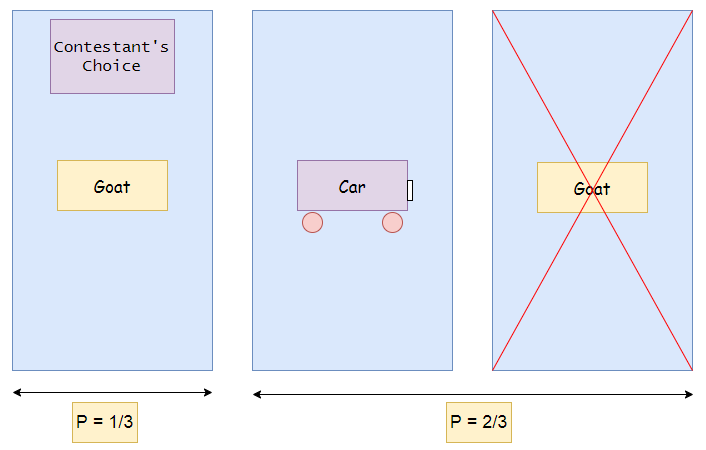
在上图中,我们可以看到,在主持人打开3号门后,两扇门拥有汽车的概率增加到2/3。现在我们知道第三扇门有山羊,第二扇门有车的概率增加到2/3。因此,换门更有利。
现在,我们将使用蒙特卡洛方法多次执行此测试案例,并以实验方式找出其概率。
1、导入所需的库:

2、初始化一些数据:

3、主函数:
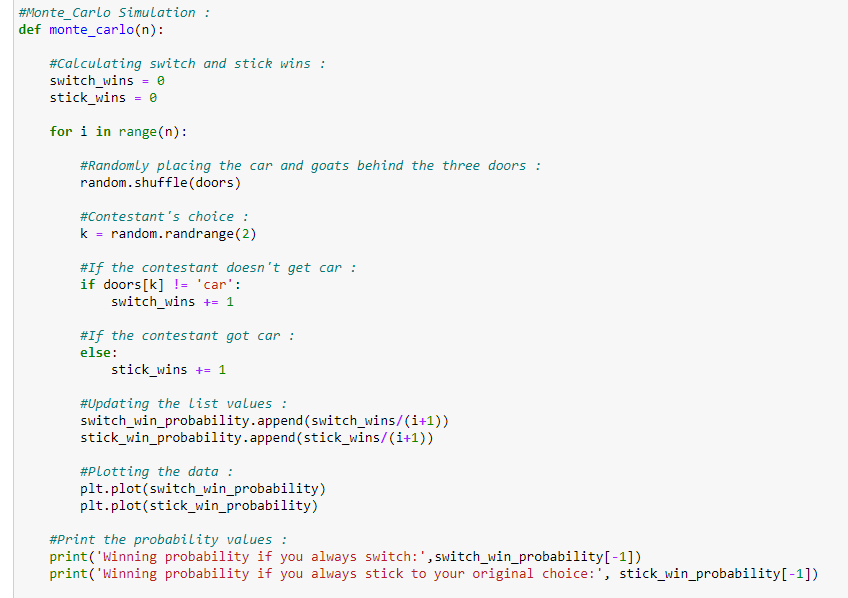
4、调用主函数:

5、输出:
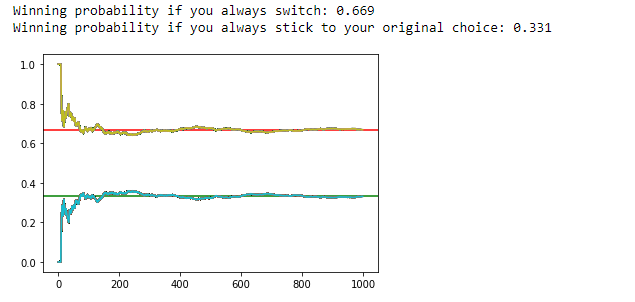
在上图 中可以看到,在 1000 次迭代后,如果我们换门,那么中奖概率为 0.669。因此,我们相信,在本例中换门对我们有利。
4、Buffon's Needle问题:
:法国贵族Buffon,在1777年发布了以下问题:
假设我们在一张划线纸上扔一根短针——针头正好跨越线的位置的可能性是多大?
概率取决于纸上线条之间的距离(d),也取决于我们扔的针的长度(l),或者更确切地说,这取决于比率l/d。对于这个例子,我们可以认为针l ≤ d。简言之,我们的目的是假设针不能同时跨越两条不同的线。令人惊讶的是,这个问题的答案涉及PI。
在这里,我们将使用蒙特卡洛方法。然而,在进入之前,我们将展示解决方案是如何产生的,这使其更有趣。
定理:
如果一根长度为 l 的短针掉在用同样间隔的距离 d ≥ l 的划线的纸上,则针头恰好穿过其中一条线的概率是:
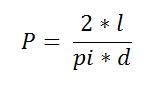
证明:
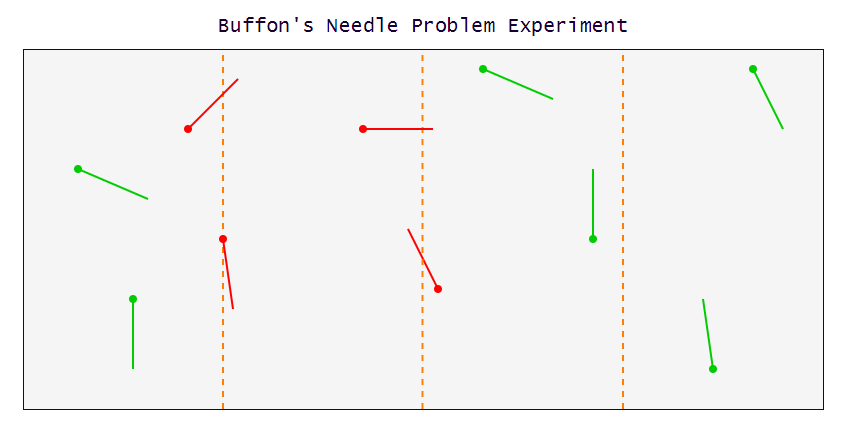
接下来,我们需要计算跨越任何垂直线的针数量。对于与其中一条线相交的针,对于该线的特定值,以下是针头可能与垂直线相交的最大值和最小值。
1、最大可能值:
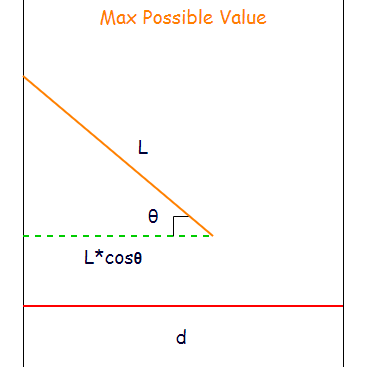
2、最小可能值:
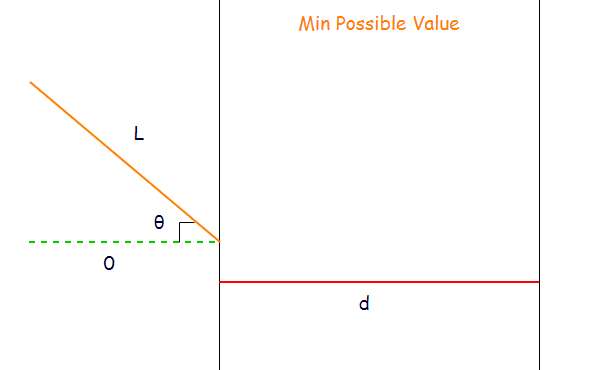
此,对于theta的特定值,针头位于垂直线的概率是:
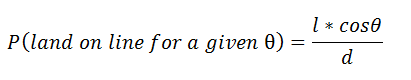
上述概率公式仅限于theta的一个值:在我们的实验中,theta的价值范围从0到pi/2。接下来,我们将通过整合其所有可能值来找到实际概率。
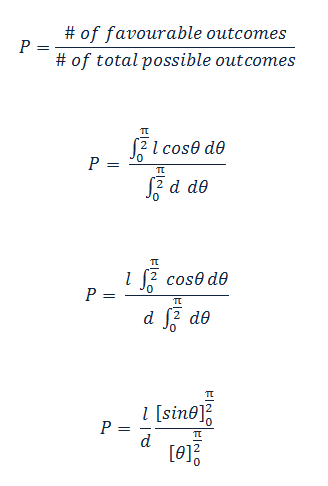
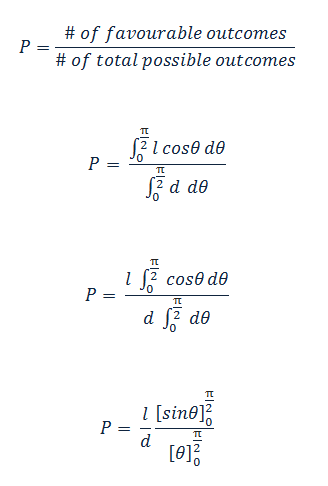
接下来,我们将使用上述公式来通过实验找出PI的值。
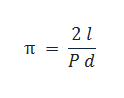
现在,请注意,我们有 l 和 d 值。我们的目标是首先找到 P 的值,以便得到 PI 的价值。要找到概率 P,我们需要跨线针数量和针的总数。由于我们已经有针总数,我们现在唯一需要的就是跨线针的计数。
下图展示了我们将如何计算跨线针的数量:
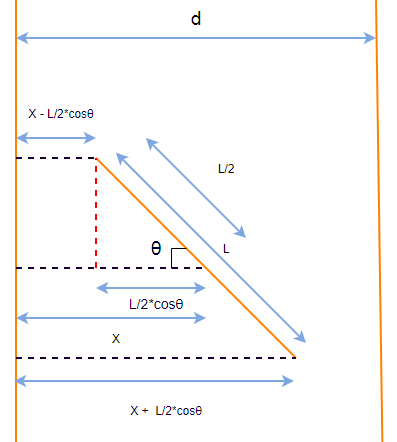
1、导入所需的库:

2、主函数:

3、调用主函数:

4、输出:
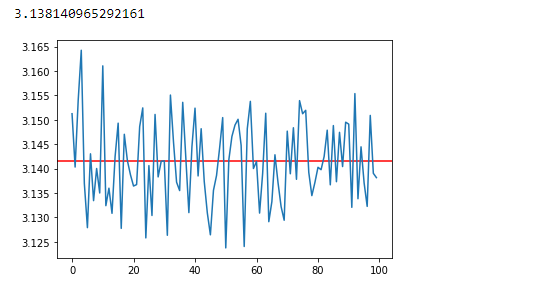
如上图所示,经过100次迭代后,我们能够使用蒙特卡洛方法获得非常接近的PI值。
5、为什么庄家总是赢?
赌场如何赚钱?诀窍很简单 —— "你玩得越多, 赌场赚得越多。让我们通过一个简单的蒙特卡洛模拟示例来看看其运作原理。
考虑一个假想的游戏,玩家必须从一袋芯片中挑一个芯片。
规则:
- 袋子里装着1~100个芯片。
- 用户可以投注芯片数量为偶数或奇数。
- 在这个游戏中,10和11是特殊数字。如果我们押注于偶数,则 10 将计为奇数,如果我们押注奇数,则 11 将计为偶数。
- 如果我们押注偶数, 我们得到 10, 那么我们输了。
- 如果我们押注奇数, 我们得到 11, 那么我们输了。
如果我们押注奇数,我们获胜的概率为49/100。庄家获胜的概率是51/100。因此,对于一个奇数赌注,庄家的利润是 = 51/100- 49/100 = 200/10000 = 0.02 = 2%
如果我们押注于偶数,用户获胜的概率为 49/100。庄家获胜的概率是51/100。因此,对于一个偶数赌注,庄家的利润是 = 51/100-49/100 = 200/10000 = 0.02 = 2%
总之,每下1美元的赌注,其中0.02美元就归庄家的。相比之下,轮盘赌庄家的最低利润为2.5%。因此,我们确信,在假想的比赛中,你比轮盘赌更有可能获胜。
1、导入需要的库:

2、玩家下注:
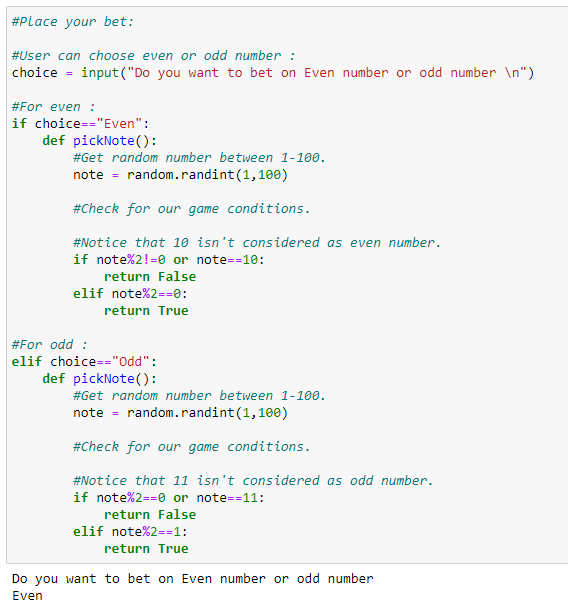
3、主函数:

4、最终输出:
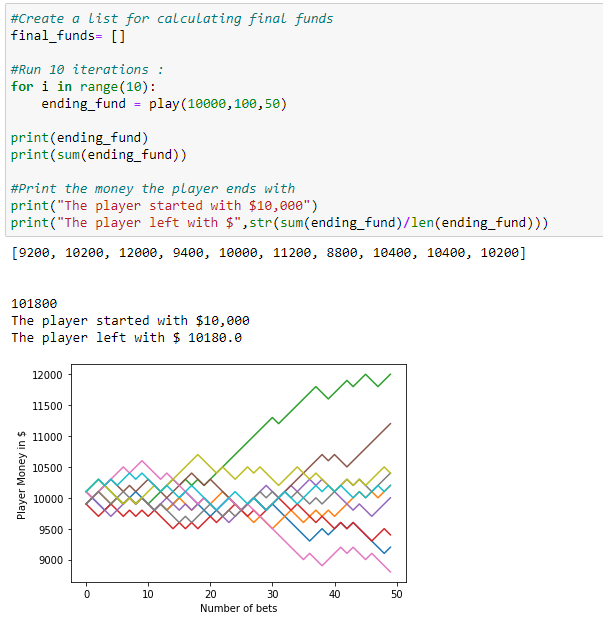
5、运行1000次:
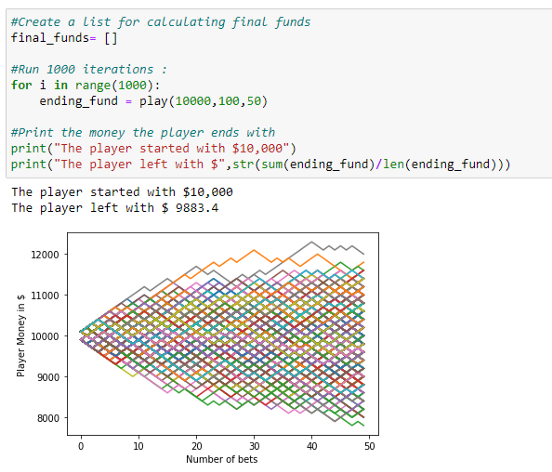
6、下注次数 = 5:
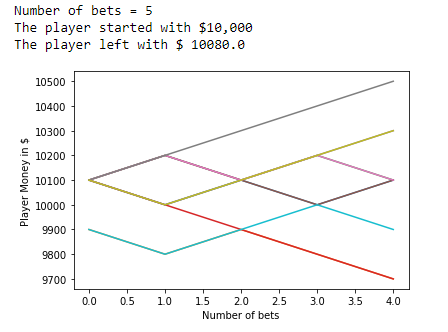
7、下注次数 = 10:
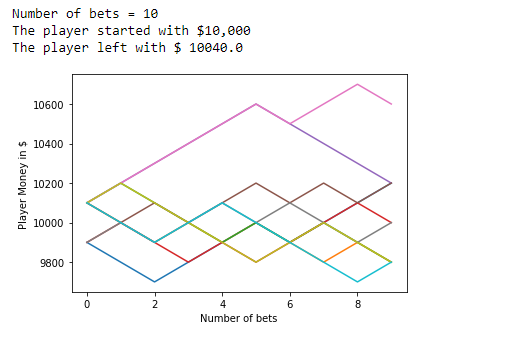
8、下注次数 = 1000:
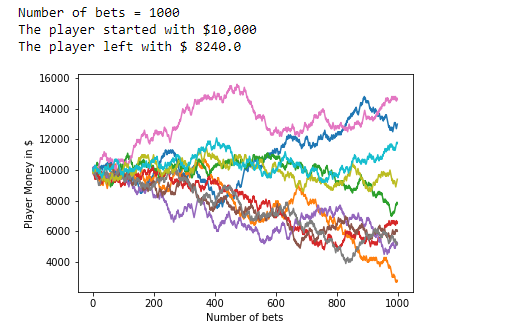
9、下注次数 = 5000:
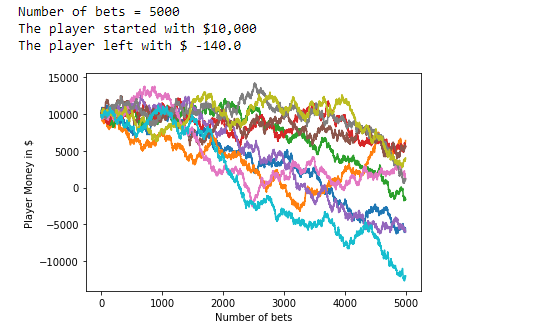
10、下注次数 =10000:
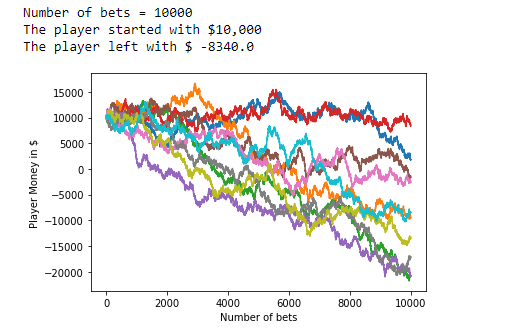
从上述实验中,我们可以看到,如果玩家在这些游戏上的投注更少,他们更有可能盈利。在某些情况下,我们得到负数,这意味着玩家失去了所有的钱,并累积了债务而不是盈利。
6、结论
与任何预测模型一样,仿真最多做到和我们估计一样好。重要的是要记住,蒙特卡洛仿真只代表概率,而不是确定性。然而,蒙特卡洛仿真在预测未知的未来时可能是一个有价值的工具。
原文链接:Monte Carlo Simulation An In-depth Tutorial with Python
BimAnt翻译整理,转载请标明出处





