NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 - 3D道路快速建模
这篇文章详细介绍了三次曲线、贝塞尔曲线和 B 样条曲线和曲面背后的数学原理,并提供了使用 Three.js 库实现的代码。
1、简介
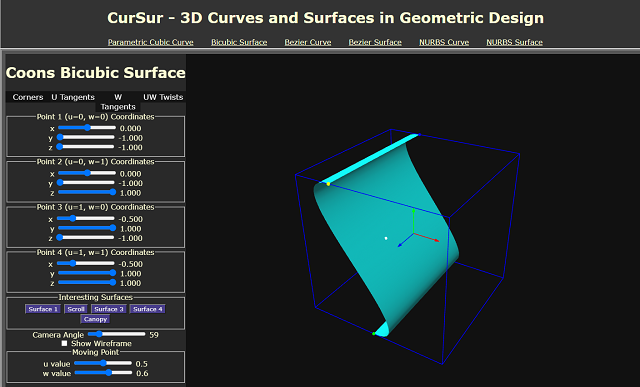
你可以在这里访问上图应用程序。此应用程序名为 CurSur,是 Curves and Surfaces 的简称。原始代码可以在这里获取。
在几何设计中,有多种类型的曲线和曲面 - 2D 和 3D。其中,在几何建模的入门课程中,通常教授三种类型——三次曲线、贝塞尔曲线和B样条曲线和曲面。本文的目的是介绍如何使用Three.js 库在浏览器中绘制这些 3D 曲线和曲面的程序。
在本文中,我们将介绍如何使用 Three.js 在浏览器中以 3D 方式绘制直线和曲面,以及如何修改这些曲线和曲面的控制点和切线(导数)等几何参数。这里给出的代码的主要要求是:
- 应该在屏幕上显示这六种 3D 曲线和曲面 - Parametric Cubic Curve、Coons Bicubic Surface、Bezier Curve、Bezier Surface、B-Spline(实际上是 NURBS)Curve 和 NURBS Surface。
- 应允许用户修改控制点的 x、y、z 坐标,和/或相对于曲线或曲面的 x、y、z(切线)的导数,并查看曲线或曲面如何动态修改屏幕。
- 还应使用户能够在线框模式下查看表面。
- 应显示曲线或曲面的边界框,其尺寸为 2 个单位,以原点为中心。
- 应允许用户修改摄像机角度,使摄像机绕垂直轴旋转,围绕正在查看的场景。
- 应使用户能够修改参数值 - u 在曲线的情况下,u,w 在曲面的情况下,并看到相应的点在曲线和曲面上随着这些 u,w 值的变化而移动。
- 单击按钮应显示一些标准曲线和曲面。
- 应该使用 Three.js 库在屏幕上显示 3D 曲线或曲面。
- 应该使用 Vanilla JS 而不是任何框架。
- 不应有文本框类型的用户输入,所有用户交互都应仅通过滑块、复选框、组合框和按钮。
2、参数化曲线曲面简介
我们在高中和中级大学了解到直线有笛卡尔和极坐标形式的表示形式,例如直线、圆弧、圆锥曲线等。然而,出于几何设计的目的,笛卡尔和极坐标形式通常不是首选,原因有很多,其中两个是 (i) 用笛卡尔形式表示垂直或接近垂直的线并不容易,因为斜率(导数)趋向无限大,并且(ii)用这些笛卡尔和极坐标形式表示一般形状并不容易。因此,首选形式是参数化的。
在参数形式中,3D 曲线表示为:
- x = x(u)
- y = y(u)
- z = z(u)
其中x,y,z是该曲线上任意一点的3D坐标,u是一个参数,通常在0≤u≤1范围内。其中x(u),y(u),z(u)是三个参数 u 的函数。使用这种表示法,可以很容易地表示任何形状的线,并且不会像笛卡尔表示法那样存在无限导数的缺点。特别是,我们看到了 x(u)、y(u)、z(u) 的三个这样的函数,它们定义了本文中的三种曲线 - 参数三次曲线、贝塞尔曲线和 B 样条曲线。
以类似的方式,也可以使用以下等式来表示表面:
- x = x(u,w)
- y = y(u,w)
- z = z(u,w)
其中,x, y, z 通常是曲面上一点的三维坐标,u, w 是参数空间中相互垂直方向的两个参数,通常在 0 ≤ u ≤ 1, 0 ≤ w ≤ 1。在这里,三个函数 x(u,w)、y(u,w)、z(u,w) 采用三种不同的形式表示双三次、贝塞尔和 B 样条。
3、Three.js中的绘图
一条曲线被绘制为许多直线段,首尾相接以呈现平滑曲线的外观,因此,最基本的做法是在浏览器中绘制一条 3D 直线。
自 WebGL 出现以来,出现了抽象出实际 WebGL 库内部细节的 JavaScript 3D 库,其中两个流行的此类 JavaScript 库是 Three.js 和 Babylon.js。 在本文中,我使用了 Three.js 库,并将展示有关如何在屏幕上绘制线条和曲面的代码摘录。
在 Three.js 中绘制 3D 对象所需的三个最重要的实体是场景、相机和渲染器。 代码如下:
scene = new THREE.Scene();
camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000 );
renderer = new THREE.WebGLRenderer({ antialias: true });3.1 在 Three.js 中画一条直线
直线段由其在空间中的两个端点 (x1, y1, z1) 和 (x2, y2, z2) 确定。
绘制直线段,Three.js 中有一个Geometry 对象,叫做BufferGeometry。 早些时候还有一个 Geometry 对象,但在 Three.js 的修订版 125 中已弃用,将使用 BufferGeometry 对象取而代之。
此外,还要指定一种材料。 线和面有不同的材料。
使用以下代码绘制直线段:
const material = new THREE.LineBasicMaterial({ color: 0xff00ff });
const geometry = new THREE.BufferGeometry();
const vertices = [];
vertices.push(-0.75, -0.75, -0.75);
vertices.push(0.75, 0.75, 0.75);
geometry.setAttribute(
"position",
new THREE.Float32BufferAttribute(vertices, 3));
let line = new THREE.Line(geometry, material);
scene.add(line);
render();在上面的代码中,在端点(-0.75,-0.75,-0.75)和(0.75,0.75,0.75)之间绘制了一条直线,如下图洋红色线所示:
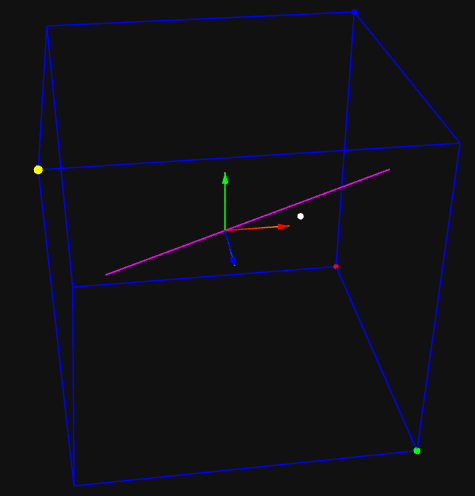
3.2 在 Three.js 中绘制一个简单的表面
一个表面被定义为一组三角形。 因此,要绘制的基本几何实体是三角形。 3D 中的三角形由其三个顶点 (x1, y1, z1)、(x2, y2, z2) 和 (x3, y3, z3) 指定。 我们不能只绘制定义三角形的三条直线,因为那样会显示为线框图。
如果场景只包含一组线段,则不需要额外的光来照亮场景。 但是,如果场景中有表面或 3D 对象(如立方体、球体等),则必须指定一盏或多盏灯。 有不同类型的灯,这些在 Three.js 文档中定义。 向场景添加几个灯的代码如下所示:
scene.add(new THREE.HemisphereLight(0x606060, 0x404040));
// White directional light at 0.65 intensity shining from the top.
let directionalLight = new THREE.DirectionalLight(0xffffff, 0.65);
scene.add(directionalLight);要将三角形指定为曲面,我们需要定义三角形的法线。 现在,三角形有两条法线,都指向相反的方向。 如果材质指定为双面,则三角形的两边都将显示,并定义了灯光。 但是,如果表面指定为单面,则光线未照射到的一侧不太可能被照亮。
在场景中绘制三角面的代码如下所示:
function computeCoonsBicubicSurface() {
setupFourPoints();
surfacePoints.length = 0;
let uVal, wVal;
for (let j = 0; j <= noDivisions; ++j) {
wVal = j * step;
for (let i = 0; i <= noDivisions; ++i) {
uVal = i * step;
let pt = computePointOnSurface(uVal, wVal);
surfacePoints.push(pt.xVal, pt.yVal, pt.zVal);
}
}
renderCoonsBicubicSurface();
handleUWValue();
}
function renderCoonsBicubicSurface() {
scene.remove(surfaceMesh);
scene.remove(lineWire);
let material = new THREE.MeshStandardMaterial({
side: THREE.DoubleSide,
color: 0x00ffff,
emissive: 0x111111,
dithering: true,
flatShading: false,
roughness: 1,
metalness: 0.15,
skinning: true,
});
let materialLine = new THREE.LineBasicMaterial({
color: 0x00ffff,
});
let geometry = new THREE.BufferGeometry();
const indices = [];
indices.length = 0;
for (let i = 0; i < noDivisions; i++) {
for (let j = 0; j < noDivisions; j++) {
const a = i * (noDivisions + 1) + (j + 1);
const b = i * (noDivisions + 1) + j;
const c = (i + 1) * (noDivisions + 1) + j;
const d = (i + 1) * (noDivisions + 1) + (j + 1);
// generate two faces (triangles) per iteration
indices.push(a, b, d); // face one
indices.push(b, c, d); // face two
}
}
geometry.setIndex(indices);
geometry.setAttribute(
"position",
new THREE.Float32BufferAttribute(surfacePoints, 3).onUpload(disposeArray)
);
geometry.computeVertexNormals();
surfaceMesh = new THREE.Mesh(geometry, material);
scene.add(surfaceMesh);
let surfaceWire = new THREE.WireframeGeometry(geometry);
lineWire = new THREE.LineSegments(surfaceWire, materialLine);
scene.add(lineWire);
render();
}其中 surfacePoints 是上面定义的点数组。 使用上述代码绘制的表面如下所示。 随着三角形数量的增加,表面开始呈现出光滑的外观。 请查看文件 script2.js 以获取完整代码。

4、参数化三次曲线
参数三次曲线由以下三个方程定义:
x(u) = B0x + B1x u + B2x u2 + B3x u3
y(u) = B0y + B1y u + B2y u2 + B3y u3
z(u) = B0z + B1z u + B2z u2 + B3z u3这里,12个常数B0x、B1x、B2x、B3x、B0y、B1y、B2y、B3y、B0z、B1z、B2z、B3z是根据曲线上的点确定的常数。
有两种方法可以确定这些常数:
- 四点式:如果已知曲线上的四个点,则这四个点的坐标指定十二个方程来确定十二个常数。
- Hermite 形式:如果两个端点的坐标已知,并且两个端切线(相对于端点处的 x、y、z 的导数)已知,则这些也指定十二个方程来确定十二个常数
这是本文随附的应用程序中介绍的两种方法。对应于这两种形式的方程的推导在 Mortenson 的几何建模一书中或 Rogers 和 Adams 的计算机图形学的数学元素一书中给出。对于Hermite Form,x,y,z方程关于x,y,z坐标的导数,这些在上面提到的书中也给出了。
4.1 四点式
对于这个四点形式,我们需要指定四个点的 u 值。 出于此代码的目的,我们将这些取为 0、1/3、2/3 和 1。对于参数 u 的这些值,将它们代入曲线方程,可以确定常数 Bij 的值。 当使用坐标值的滚动条改变四个点中任何一个的坐标值时,动态计算这些常数 Bij,计算曲线上所有点的新坐标,并在屏幕上刷新曲线。 代码是:
function computePointFourPointForm(uVal) {
let u2, u3;
let coeff1, coeff2, coeff3, coeff4;
let xCurve, yCurve, zCurve;
u2 = uVal * uVal;
u3 = u2 * uVal;
// This is the Four Point Formula from Mortenson's book on Geometric Modeling
// For values of u being 0, 1/3, 2/3 and 1.
coeff1 = -4.5 * u3 + 9 * u2 - 5.5 * uVal + 1;
coeff2 = 13.5 * u3 - 22.5 * u2 + 9 * uVal;
coeff3 = -13.5 * u3 + 18 * u2 - 4.5 * uVal;
coeff4 = 4.5 * u3 - 4.5 * u2 + uVal;
xCurve = p1x * coeff1 + p2x * coeff2 + p3x * coeff3 + p4x * coeff4;
yCurve = p1y * coeff1 + p2y * coeff2 + p3y * coeff3 + p4y * coeff4;
zCurve = p1z * coeff1 + p2z * coeff2 + p3z * coeff3 + p4z * coeff4;
return {
xVal: xCurve,
yVal: yCurve,
zVal: zCurve,
};
}4.2 Hermite形式
对于这种形式,指定了两个端点和在这些端点处的两组导数,这些用于计算常数 Bij。 这些也是来自摩顿森书中给出的公式。 代码是:
function computePointHermiteForm(uVal) {
let u2, u3;
let coeff1, coeff2, coeff3, coeff4;
let xCurve, yCurve, zCurve;
u2 = uVal * uVal;
u3 = u2 * uVal;
// This is the Hermite Formula from Mortenson's book on Geometric Modeling
// u and du at the endpoints.
coeff1 = 2 * u3 - 3 * u2 + 1;
coeff2 = -2 * u3 + 3 * u2;
coeff3 = u3 - 2 * u2 + uVal;
coeff4 = u3 - u2;
xCurve = p1xh * coeff1 + p2xh * coeff2 + p1dxh * coeff3 + p2dxh * coeff4;
yCurve = p1yh * coeff1 + p2yh * coeff2 + p1dyh * coeff3 + p2dyh * coeff4;
zCurve = p1zh * coeff1 + p2zh * coeff2 + p1dzh * coeff3 + p2dzh * coeff4;
return {
xVal: xCurve,
yVal: yCurve,
zVal: zCurve,
};
}当用户使用屏幕上的滚动条修改终点坐标和导数对应的滚动条时,动态计算常数B ij ,重新计算整条曲线。
4.3 参数三次曲线的代码
曲线呈现为曲线上的一组直线段。 将整个参数范围0≤u≤1分成若干部分,所有的直线段画成一个环。 其代码在文件 script1.js 中。 相应的 HTML 位于文件 page1.html 中。
let curvePoints = [];
curvePoints.length = 0;
for (let i = 0; i < noUPoints; ++i) {
uVal = uStep * i; // uVal and uStep are defined earlier
let pt = computePointFourPointForm(uVal);
// let pt = computePointHermiteForm(uVal);
curvePoints.push(pt.xVal, pt.yVal, pt.zVal);
}4.4 验证
为了验证,使用了一组点坐标/导数的标准值,并且可以看到生成的曲线的形状。此外,通过改变参数 u 获得的曲线上的点显示在屏幕上,并用于验证。
这里要注意的一个有趣案例是非线性直线。通常情况下,对于参数 u 的相等增量,沿曲线经过的距离相等,这通常是不正确的。这将非线性元素引入参数化三次曲线。这是一条非线性直线。即使这些点都位于同一条直线上,但不同的参数增量会导致沿该直线的遍历距离不同。
在 Hermite 形式中,对于直线,可能会发生端点导数位于直线段之外的方向。在这种情况下,将参数 u 从 0 增加到 1 后,该点会超出直线段,然后反转方向,然后向第二个端点移动。这又是一条非线性直线。
一些这样的情况在屏幕上以指定有趣曲线的按钮的形式给出。
5、3D 贝塞尔曲线
上图的Parametric Cubic Curve,尤其是Four Point Form中,曲线通过了所有的四个点,属于曲线拟合的一种形式。 贝塞尔曲线由 P Bezier 引入,他根据控制点定义了曲线方程。 贝塞尔曲线由这个等式定义

在我们的应用程序中,我们考虑了具有 5 个控制点的贝塞尔曲线,因此多项式中 u 的最高次数为 4。
5.1 贝塞尔曲线代码
与参数三次曲线的情况一样,贝塞尔曲线也呈现为曲线上的一组直线段。 将整个参数范围0≤u≤1分成若干部分,所有的直线段画成一个环。 其代码在文件 script3.js 中,它对应于 HTML 文件 page3.html:
u2 = uVal * uVal;
u3 = u2 * uVal;
u4 = u3 * uVal;
// This is the Bezier Curve Formula from Rogers and Adam's Book - Mathematical Elements for
// Computer Graphics
coeff1 = u4 - 4 * u3 + 6 * u2 - 4 * uVal + 1;
coeff2 = -4 * u4 + 12 * u3 - 12 * u2 + 4 * uVal;
coeff3 = 6 * u4 - 12 * u3 + 6 * u2;
coeff4 = -4 * u4 + 4 * u3;
coeff5 = u4;
xCurve = p1x * coeff1 + p2x * coeff2 + p3x * coeff3 + p4x * coeff4 + p5x * coeff5;
yCurve = p1y * coeff1 + p2y * coeff2 + p3y * coeff3 + p4y * coeff4 + p5y * coeff5;
zCurve = p1z * coeff1 + p2z * coeff2 + p3z * coeff3 + p4z * coeff4 + p5z * coeff5;5.2 验证
贝塞尔曲线有以下验证方面:
- 在一般情况下,曲线应该通过端点,而不是通过其他控制点。
- 但是,当所有的控制点都在一条直线上时,曲线也应该是通过这些点的直线。
- 端点处曲线的切线应与连接该特定端点及其下一个控制点的线一致。 例如,在曲线的起点,曲线的切线应与连接第一和第二控制点的直线一致。 同样在结束控制点。
所有这些点都针对贝塞尔曲线进行了验证,并绘制了一组有趣的贝塞尔曲线,每条曲线在屏幕上都有自己的按钮。
6、3D 中的 NURBS 曲线
NURBS 代表非均匀有理 B 样条曲线。出现这种曲线的必要性是因为参数立方曲线和贝塞尔曲线都不允许对曲线进行局部控制。换句话说,对于参数三次曲线和贝塞尔曲线,修改一个控制点会修改整条曲线,这在许多应用程序中都是不可取的。另一方面,B 样条曲线允许对曲线进行局部控制。修改控制点的坐标会导致仅在该控制点附近修改曲线,而曲线的其余部分不受影响。
有理 B 样条曲线的一般方程如下:

NURBS 曲线的阶数不依赖于控制点的数量。这两个是 NURBS 曲线中的独立实体。
在我们的应用程序中,我们最初定义了六个控制点,并允许用户添加控制点(最多总共 20 个控制点),并修改每个控制点的坐标(x、y、z、h 值)点,并可视化生成的 NURBS 曲线。
6.1 Nurbs 曲线代码
由于 Three.js 已经有 NURBS 曲线的开源代码,我们不打算重新发明轮子。 因此,在这里,我们从那里提取了 NURBS 曲线代码的相关内容,并将其包含在名为 NurbsHelper.js 的文件中。
在我们的代码中,为了指定控制点,我们将它们生成为以原点为中心的 2 维边界框内的随机数。
尽管实际上 NURBS 曲线是我们应用程序中三个曲线中最复杂的一个,但它的代码 - script5.js 是最简单的,它只调用文件 NurbsHelper.js 中的相关函数。 对应的 HTML 文件是 page5.html。
6.2 验证
- 如上所述,NURBS 曲线允许局部控制,这意味着通过修改一个点的坐标 (x, y, z, h),曲线仅在局部进行修改,而曲线的另一部分保持不变。 这是一个可以很容易地通过视觉验证的属性。
- 还有一点需要验证的是,通过修改一个控制点的齐次坐标h的值。 这应该将曲线拉向该控制点。 这也从视觉上得到了验证。
- 另一个验证点是修改曲线的度数。 对于等于 1 的度数,曲线类似于控制多边形本身。 随着曲线度数的增加,曲线远离控制点(端点除外),对于这些度数的较高值,曲线离其相应的控制点最远。
7、Coons双三次曲面
参数三次曲线的二维等价物是库恩斯双三次曲面。这种曲面的方程如下:

在参数空间中,有两个参数 u 和 w,它们在 [0, 1] 范围内变化。需要为 Coons 双三次曲面定义以下边界条件:
- 矩形面片的四个端点。
- 在这些端点处关于参数 u 的切向量。这些是关于 u 的偏导数。
- 在这些端点处关于参数 w 的切向量。这些是关于 w 的偏导数。
- 在这些端点处相对于参数 u、w 扭曲向量。这些是关于 u 和 w 的偏导数。
当上述任何一项发生变化时,表面都会发生变化。
所有这些如下图所示:

补丁的边界是这四个曲线:
- u 增加且 w 为 0 的曲线。
- w 递增且 u 为 0 的曲线。
- u 增加且 w 为 1 的曲线。
- w 递增且 u 为 1 的曲线。
7.1 Coons 双三次曲面代码
以下 JavaScript 函数在文件 script2.js 中计算曲面上的一个点。
function computePointOnSurface(uVal, wVal) {
let u2, u3, w2, w3;
let f1u, f2u, f3u, f4u, f1w, f2w, f3w, f4w;
let valueX, valueY, valueZ;
let valx1, valx2, valx3, valx4;
let valy1, valy2, valy3, valy4;
let valz1, valz2, valz3, valz4;
w2 = wVal * wVal;
w3 = w2 * wVal;
f1w = 2.0 * w3 - 3 * w2 + 1.0;
f2w = -2.0 * w3 + 3.0 * w2;
f3w = w3 - 2.0 * w2 + wVal;
f4w = w3 - w2;
u2 = uVal * uVal;
u3 = u2 * uVal;
f1u = 2.0 * u3 - 3 * u2 + 1.0;
f2u = -2.0 * u3 + 3.0 * u2;
f3u = u3 - 2.0 * u2 + uVal;
f4u = u3 - u2;
valx1 = f1u * (p1x * f1w + p2x * f2w + p1wx * f3w + p2wx * f4w);
valx2 = f2u * (p3x * f1w + p4x * f2w + p3wx * f3w + p4wx * f4w);
valx3 = f3u * (p1ux * f1w + p2ux * f2w + p1uwx * f3w + p2uwx * f4w);
valx4 = f4u * (p3ux * f1w + p4ux * f2w + p3uwx * f3w + p4uwx * f4w);
valueX = valx1 + valx2 + valx3 + valx4;
valy1 = f1u * (p1y * f1w + p2y * f2w + p1wy * f3w + p2wy * f4w);
valy2 = f2u * (p3y * f1w + p4y * f2w + p3wy * f3w + p4wy * f4w);
valy3 = f3u * (p1uy * f1w + p2uy * f2w + p1uwy * f3w + p2uwy * f4w);
valy4 = f4u * (p3uy * f1w + p4uy * f2w + p3uwy * f3w + p4uwy * f4w);
valueY = valy1 + valy2 + valy3 + valy4;
valz1 = f1u * (p1z * f1w + p2z * f2w + p1wz * f3w + p2wz * f4w);
valz2 = f2u * (p3z * f1w + p4z * f2w + p3wz * f3w + p4wz * f4w);
valz3 = f3u * (p1uz * f1w + p2uz * f2w + p1uwz * f3w + p2uwz * f4w);
valz4 = f4u * (p3uz * f1w + p4uz * f2w + p3uwz * f3w + p4uwz * f4w);
valueZ = valz1 + valz2 + valz3 + valz4;
return {
xVal: valueX,
yVal: valueY,
zVal: valueZ,
};
}7.2 验证
以下是验证方面:
- 当使用它们的滑块改变边界点的坐标时,相应的边界点应该在指定的 x、y 或 z 方向上变化,并且表面应该相应地改变。
- 当使用滑块更改 u 或 v 方向的切线矢量时,也会发生同样的情况,尽管这种变化不像更改坐标值时那样明显。
- 类似地,当扭曲向量发生变化时,曲面也应该发生变化。
- 还显示了一些预定义的表面,这些表面在单击左窗格底部的按钮时出现。
8、贝塞尔曲面
贝塞尔曲线的二维(在参数空间中)等价物是贝塞尔曲面。 这种表面的方程式如下:

8.1 贝塞尔曲面的代码
以下 JavaScript 函数在文件 script4.js 中计算贝塞尔曲面上的一个点。 出于本文的目的,所提供的代码适用于 4 x 4 贝塞尔曲面,共有 16 个控制点。 对应的 HTML 文件是 page4.html。
function computeBezierSurfacePoint(uVal, wVal) {
let u2, u3, w2, w3;
u2 = uVal * uVal;
u3 = uVal * u2;
w2 = wVal * wVal;
w3 = wVal * w2;
// Need to note the following regarding THREE.js Matrix4.
// When we set the matrix, we set it in row major order.
// However, when we access the elements of this matrix, these are
// returned in column major order.
let matC = new THREE.Matrix4();
matC.set(-1, 3, -3, 1, 3, -6, 3, 0, -3, 3, 0, 0, 1, 0, 0, 0);
let matPx = new THREE.Matrix4();
matPx.set(
p00x, p10x, p20x, p30x, p01x, p11x, p21x, p31x,
p02x, p12x, p22x, p32x, p03x, p13x, p23x, p33x
);
let matPy = new THREE.Matrix4();
matPy.set(
p00y, p10y, p20y, p30y, p01y, p11y, p21y, p31y,
p02y, p12y, p22y, p32y, p03y, p13y, p23y, p33y
);
let matPz = new THREE.Matrix4();
matPz.set(
p00z, p10z, p20z, p30z, p01z, p11z, p21z, p31z,
p02z, p12z, p22z, p32z, p03z, p13z, p23z, p33z
);
let mat1x = new THREE.Matrix4();
mat1x.multiplyMatrices(matC, matPx);
let mat1y = new THREE.Matrix4();
mat1y.multiplyMatrices(matC, matPy);
let mat1z = new THREE.Matrix4();
mat1z.multiplyMatrices(matC, matPz);
let mat2x = new THREE.Matrix4();
mat2x.multiplyMatrices(mat1x, matC);
let mat2y = new THREE.Matrix4();
mat2y.multiplyMatrices(mat1y, matC);
let mat2z = new THREE.Matrix4();
mat2z.multiplyMatrices(mat1z, matC);
// We access the matrix elements in column major order.
let ex = mat2x.elements;
let w0x = ex[0] * w3 + ex[4] * w2 + ex[8] * wVal + ex[12];
let w1x = ex[1] * w3 + ex[5] * w2 + ex[9] * wVal + ex[13];
let w2x = ex[2] * w3 + ex[6] * w2 + ex[10] * wVal + ex[14];
let w3x = ex[3] * w3 + ex[7] * w2 + ex[11] * wVal + ex[15];
let ey = mat2y.elements;
let w0y = ey[0] * w3 + ey[4] * w2 + ey[8] * wVal + ey[12];
let w1y = ey[1] * w3 + ey[5] * w2 + ey[9] * wVal + ey[13];
let w2y = ey[2] * w3 + ey[6] * w2 + ey[10] * wVal + ey[14];
let w3y = ey[3] * w3 + ey[7] * w2 + ey[11] * wVal + ey[15];
let ez = mat2z.elements;
let w0z = ez[0] * w3 + ez[4] * w2 + ez[8] * wVal + ez[12];
let w1z = ez[1] * w3 + ez[5] * w2 + ez[9] * wVal + ez[13];
let w2z = ez[2] * w3 + ez[6] * w2 + ez[10] * wVal + ez[14];
let w3z = ez[3] * w3 + ez[7] * w2 + ez[11] * wVal + ez[15];
let qx = u3 * w0x + u2 * w1x + uVal * w2x + w3x;
let qy = u3 * w0y + u2 * w1y + uVal * w2y + w3y;
let qz = u3 * w0z + u2 * w1z + uVal * w2z + w3z;
return {
xVal: qx,
yVal: qy,
zVal: qz,
};
}8.2 验证
- 同样,当任何控制点(坐标)发生变化时,相应的表面也应发生变化。 这可以通过查看渲染的表面来验证。
- 显示了许多有趣的表面,可通过单击它们的按钮获得。
9、NURBS曲面
NURBS 曲线的二维(在参数空间中)等价物是 NURBS 曲面。 NURBS 曲面相对于其他两种曲面的优势在于 NURBS 曲面提供了对曲面的局部控制。修改控制点的坐标只会影响该控制点附近的表面,而表面的其余部分不受影响。这是因为对应于 NURBS 曲面的基函数。
9.1 NURBS 曲面代码
Three.js 库的创建者再次提供了一个 JavaScript 文件来计算 NURBS 曲面上一个点的坐标,我们从那里提取了相关内容,并将其用于此应用程序。它们位于 NurbsHelper.js 文件中。与 NURBS 曲线的情况一样,定义了 u 和 w 方向的两个结向量。
在此应用程序中,我们定义了一个在 u 和 w 方向各有 7 个控制点的 NURBS 曲面。因此,共有 49 个控制点可供用户修改。对于这些控制点中的每一个,用户都可以在范围内更改 x、y、z、h 值。
NURBS Surface的计算代码在文件script6.js中,如下。 HTML 是 page6.html。
function computeNurbsSurface() {
nurbsSurface = new NURBSSurface(
degreeU,
degreeW,
knotVectorU,
knotVectorW,
points
);
surfacePoints.length = 0;
let uVal, wVal;
for (let j = 0; j <= noDivisions; ++j) {
wVal = j * step;
for (let i = 0; i <= noDivisions; ++i) {
uVal = i * step;
let pt = new Vector3();
nurbsSurface.getPoint(uVal, wVal, pt);
//let poi = new THREE.Vector3();
surfacePoints.push(pt.x, pt.y, pt.z);
}
}
renderNurbsSurface();
}10、兴趣点
我的意图是将每种类型的曲线/曲面都放在自己的文件夹中,独立包含自己的 HTML 和 JS 文件。这是使它们各自的逻辑彼此分离的方式。它们都引用相同的 three.min.js 文件,即 WebGL 库文件。此外,它们都引用相同的 style.css 文件。
因此,安排是有六个不同的文件夹,p01CubicCurve、p02CubicSurface、p03BezierCurve、p04BezierSurface、p05NurbsCurve和p06NurbsSurface。每个文件夹都有其 HTML 和 JS 文件。
另外还有一个js文件夹,里面有三个文件,three.min.js、script.js和NurbsHelper.js。
通过上面的代码安排,可能会有一些代码重复。例如,绘制边界框的那部分代码在六个 JS 文件中被复制了六次,script1.js、script2.js、script3.js、script4.js、script5.js、script6.js。我保留了它是故意这样的,因为任何想要获取这些单独文件的学习者现在都可以从它们单独的文件夹中获取它们并直接在他们的应用程序中使用它们,而无需集成代码的麻烦。这些文件夹之外唯一需要获取的代码是 three.min.js 缩小库文件和 CSS 文件。
你可能会注意到,应用程序中没有文本框类型的输入。用户交互仅通过滑块、复选框、组合框和按钮发生。这是我对软件进行防错的方法。我希望你不会“崩溃”这个应用程序。如果您遇到此应用程序崩溃、屏幕变黑或出现其他形式的不当行为的情况,请随时通过下面的评论部分通知我。
使用最新版本的 Three.js(版本 125),对几何图形的处理方式进行了重大更改。他们删除了 THREE.Geometry 并引入了 THREE.BufferGeometry。由于我不希望对 Three.js 库进行任何进一步的修改以影响我的代码的行为,因此我在代码中包含了该库的缩小版本。这样,代码是独立的,可以在没有 Internet 连接的情况下使用本地服务器运行。
该应用程序本身有一个简单直观的用户界面,没有任何多余的装饰和花哨的东西。有一个菜单,可以在其中选择所需的曲线和曲面类型。选择菜单项后,菜单下方会出现相应的屏幕。左侧窗格中是滑块和其他控件,用于修改右侧 HTML Canvas 元素上的 3D 对象。用户不能直接与 Canvas 元素交互,只能通过左侧的控件进行交互。
这里描述的数学并不新鲜,已有四十多年的历史了。有许多应用此数学来创建几何模型的软件包。然而,这里展示的打包方式,以一种在完全客户端 JavaScript 代码中运行的自包含方式,似乎是新的。
下面给出了一些可以使用此应用程序设计的表面的图库:

11、结束语
在本文中,我们描述并演示了使用 Three.js 库在浏览器上以 3D 方式绘制这六个几何对象的代码 - 参数立方曲线、贝塞尔曲线、NURBS 曲线、库恩斯双三次曲面、贝塞尔曲面和 NURBS 曲面.该应用程序允许您修改各个控制点的坐标(在范围内),在某些情况下,还可以修改切线(导数)的方向。用户还可以在线框中查看曲面,并更改相机角度,从不同方向查看曲线或曲面。所有这些都是用纯 Vanilla JavaScript 编码的,我已经在 Chrome、Safari 和 Edge 浏览器上对其进行了测试。
我喜欢编写这段代码的每一点,尤其是第一次在 3D 屏幕上移动滑块时,当滑块移动时,我感到非常激动。我希望你喜欢使用该应用程序,并在使用滑块更改控制点时查看这些动态变化的曲线和曲面。
原文链接:CurSur - 3D Curves and Surfaces in Geometric Design, in WebGL
BimAnt翻译整理,转载请标明出处





